【题目】如图所示,用三种大小不同的5个正方形和一个长方形(阴影部分)拼成长方形ABCD,其中EF=2厘米,最小的正方形的边长为x厘米.
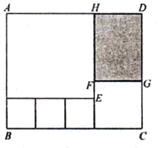
(1)用含x的代数式表示FG=________厘米,DG=________厘米.
(2)若长方形ABCD的周长等于52,求x的值
(3)若FG:DG=2:3,求四边形FGDH(阴影部分)的面积.
参考答案:
【答案】(1)(x+2);(3x-2);(2)3;(3)![]() .
.
【解析】
(1)由图可知,![]() ,GC等于最小正方形的边长与EF之和;因为最大正方形的边长是最小正方形边长的3倍,即为
,GC等于最小正方形的边长与EF之和;因为最大正方形的边长是最小正方形边长的3倍,即为![]() ,则
,则![]() ;
;
(2)由图可知,![]() ,
,![]() ,再利用长方形的周长公式列出等式,求解即可得;
,再利用长方形的周长公式列出等式,求解即可得;
(3)根据题(1)求出的用x表示的FG和DG,代入![]() 化简计算得出x的值,从而得知FG和DG的值,最后利用长方形的面积公式即可得.
化简计算得出x的值,从而得知FG和DG的值,最后利用长方形的面积公式即可得.
(1)由图可知,![]() ,GC等于最小正方形的边长与EF之和
,GC等于最小正方形的边长与EF之和
则![]()
由图可知,最大正方形的边长是最小正方形边长的3倍,即为![]()
则![]() ;
;
(2)由图可知,![]() ,
,![]()
则长方形ABCD的周长为: ![]()
由题意得:![]() ,解得:
,解得:![]() ;
;
(3)由题(1)知,![]()
代入![]() 得:
得:![]()
解得:![]()
则![]()
故四边形FGDH的面积为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场经营某种品牌的玩具,购进时的单价是30元,根据市场调查:在一段时间内,销售单价是40元时,销售量是600件,而销售单价每涨1元,就会少售出10件玩具.
(1)该玩具销售单价定为多少元时,商场能获得12000元的销售利润?
(2)该玩具销售单价定为多少元时,商场获得的销售利润最大?最大利润是多少?
(3)若玩具厂规定该品牌玩具销售单价不低于46元,且商场要完成不少于500件的销售任务,求商场销售该品牌玩具获得的最大利润是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A1,A2,A3…和B1,B2,B3,…分别在直线y=
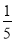 x+b和x轴上.△OA1B1,△B1A2B2,△B2A3B3,…都是等腰直角三角形如果点A1(1,1),那么点A2019的纵坐标是_____.
x+b和x轴上.△OA1B1,△B1A2B2,△B2A3B3,…都是等腰直角三角形如果点A1(1,1),那么点A2019的纵坐标是_____.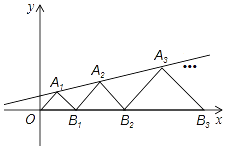
-
科目: 来源: 题型:
查看答案和解析>>【题目】书店举行购书优惠活动:
①一次性购书不超过100元,不享受打折优惠;
②一次性购书超过100元但不超过200元,一律按原价打九折;
③一次性购书超过200元,一律按原价打七折.
小丽在这次活动中,两次购书总共付款229.4元,第二次购书原价是第一次购书原价的3倍,那么小丽这两次购书原价的总和是_________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】现代互联网技术的广泛应用,催生了快递行业的高速发展,据调查,某家快递公司,今年三月份与五月份完成投递的快件总件数分别是5万件和
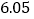 万件,现假定该公司每月投递的快件总件数的增长率相同.
万件,现假定该公司每月投递的快件总件数的增长率相同.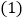 求该公司投递快件总件数的月平均增长率;
求该公司投递快件总件数的月平均增长率; 如果平均每人每月可投递快递
如果平均每人每月可投递快递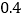 万件,那么该公司现有的16名快递投递员能否完成今年6月份的快递投递任务?
万件,那么该公司现有的16名快递投递员能否完成今年6月份的快递投递任务? -
科目: 来源: 题型:
查看答案和解析>>【题目】在Rt△ABC中,∠ABC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.
(1)证明四边形ADCF是菱形;
(2)若AC=4,AB=5,求菱形ADCF的面积.
-
科目: 来源: 题型:
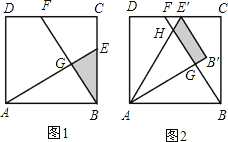
查看答案和解析>>【题目】已知:如图1,在面积为3的正方形ABCD中,E、F分别是BC和CD边上的两点,AE⊥BF于点G,且BE=1.
(1)求证:△ABE≌△BCF;
(2)求出△ABE和△BCF重叠部分(即△BEG)的面积;
(3)现将△ABE绕点A逆时针方向旋转到△AB′E′(如图2),使点E落在CD边上的点E′处,问△ABE在旋转前后与△BCF重叠部分的面积是否发生了变化?请说明理由.
相关试题

