【题目】如图,把长方形纸片![]() 纸沿对角线折叠,设重叠部分为△
纸沿对角线折叠,设重叠部分为△![]() ,那么,下列说法错误的是( )
,那么,下列说法错误的是( )
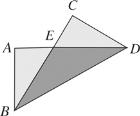
A.△![]() 是等腰三角形,
是等腰三角形,![]()
B.折叠后∠ABE和∠CBD一定相等
C.折叠后得到的图形是轴对称图形
D.△EBA和△EDC一定是全等三角形
参考答案:
【答案】B
【解析】
根据长方形的性质得到∠BAE=∠DCE=90°,AB=CD,再由对顶角相等可得∠AEB=∠CED,推出△EBA≌△EDC,根据等腰三角形的性质即可得到结论,依此可得A、C、D正确;无法判断∠ABE和∠CBD是否相等.
∵四边形ABCD为长方形
∴∠BAE=∠DCE=90°,AB=CD,
在△EBA和△EDC中,
∵∠AEB=∠CED,∠BAE=∠DCE, AB=CD,
∴△EBA≌△EDC (AAS),
∴BE=DE,
∴△EBD为等腰三角形,
∴折叠后得到的图形是轴对称图形,
故A、C、D正确,
无法判断∠ABE和∠CBD是否相等,B选项错误;
故选B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某居民小区一处圆柱形的输水管道破裂,维修人员为更换管道,需确定管道圆形截面的半径,如图是水平放置的破裂管道有水部分的截面.
(1)请你用直尺和圆规补全这个输水管道的圆形截面(保留作图痕迹);
(2)若这个输水管道有水部分的水面宽AB=8cm,水面最深地方的高度为2cm,求这个圆形截面的半径.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠B=60°,D、E分别为AB、BC上的点,且AE、CD相交于点F.若AE、CD分别为△ABC的角平分线.

(1)求∠AFC的度数;
(2)若AD=3,CE=2,求AC的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2018年“清明节”前夕,宜宾某花店用1000元购进若干菊花,很快售完,接着又用2500元购进第二批
花,已知第二批所购花的数量是第一批所购花数的2倍,且每朵花的进价比第一批的进价多
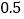 元.
元.(1)第一批花每束的进价是多少元.
(2)若第一批菊花按3元的售价销售,要使总利润不低于1500元(不考虑其他因素),第二批每朵菊花的售价至少是多少元?
-
科目: 来源: 题型:
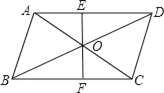
查看答案和解析>>【题目】如图平行四边形ABCD中,对角线AC,BD交于点O,EF过点O,并与AD,BC分别交于点E,F,已知AE=3,BF=5
(1)求BC的长;
(2)如果两条对角线长的和是20,求三角形△AOD的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,是一位护士统计一位病人的体温变化图,请根据统计图回答下列问题:
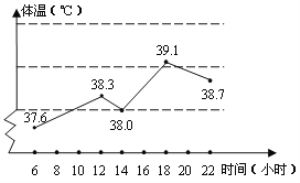
(1)病人的最高体温是达多少?
(2)什么时间体温升得最快?
(3)如果你是护士,你想对病人说____________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某县为发展教育事业,加强对教育经费投入,2012年投入3000万元,2014年投入3630万元,
(1)求该县教育经费的年平均增长率;
(2)若增长率保持不变,预计2015年该县教育经费是多少.
相关试题

