【题目】如图,一次函数y=kx+b(k≠0)的图象过点P(﹣![]() ,0),且与反比例函数y=
,0),且与反比例函数y=![]() (m≠0)的图象相交于点A(﹣2,1)和点B.
(m≠0)的图象相交于点A(﹣2,1)和点B.
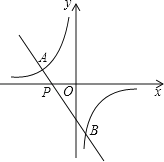
(1)求一次函数和反比例函数的解析式;
(2)求点B的坐标,并根据图象回答:当x在什么范围内取值时,一次函数的函数值小于反比例函数的函数值?
参考答案:
【答案】(1)一次函数的解析式为y=﹣2x﹣3,反比例函数的解析式为y=﹣![]() ;
;
(2)B(![]() ,﹣4),当﹣2<x<0或x>
,﹣4),当﹣2<x<0或x>![]() 时,一次函数的函数值小于反比例函数的函数值.
时,一次函数的函数值小于反比例函数的函数值.
【解析】
试题分析:(1)根据待定系数法,可得函数解析式;
(2)根据二元一次方程组,可得函数图象的交点,根据一次函数图象位于反比例函数图象的下方,可得答案.
解:(1)一次函数y=kx+b(k≠0)的图象过点P(﹣![]() ,0)和A(﹣2,1),
,0)和A(﹣2,1),
∴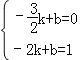 ,解得
,解得![]() ,
,
∴一次函数的解析式为y=﹣2x﹣3,
反比例函数y=![]() (m≠0)的图象过点A(﹣2,1),
(m≠0)的图象过点A(﹣2,1),
∴![]() ,解得m=﹣2,
,解得m=﹣2,
∴反比例函数的解析式为y=﹣![]() ;
;
(2)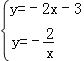 ,
,
解得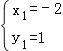 ,或
,或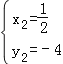 ,
,
∴B(![]() ,﹣4)
,﹣4)
由图象可知,当﹣2<x<0或x>![]() 时,一次函数的函数值小于反比例函数的函数值.
时,一次函数的函数值小于反比例函数的函数值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】以下列各组线段长为边,不能组成三角形的是( )
A. 8cm,7cm,13cm B. 6cm,6cm,12cm C. 5cm,5cm,2cm D. 10cm,15cm,17cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】某社区超市第一次用6000元购进甲、乙两种商品,其中乙商品的件数比甲商品件数的
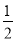 倍多15件,甲、乙两种商品的进价和售价如下表:(注:获利=售价-进价)
倍多15件,甲、乙两种商品的进价和售价如下表:(注:获利=售价-进价)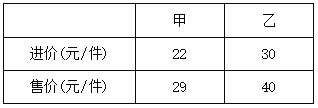
(1)该超市将第一次购进的甲、乙两种商品全部卖完后一共可获得多少利润?
(2)该超市第二次以第一次的进价又购进甲、乙两种商品.其中甲种商品的件数不变,乙种商品的件数是第一次的3倍;甲商品按原价销售,乙商品打折销售.第二次两种商品都销售完以后获得的总利润比第一次获得的总利润多180元,求第二次乙种商品是按原价打几折销售?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:用2辆A型车和1辆B型车载满货物一次可运货10吨;用1辆A型车和2辆B型车载满货物一次可运货11吨.某物流公司现有31吨货物,计划同时租用A型车a辆,B型车b辆,一次运完,且恰好每辆车都载满货物.
根据以上信息,解答下列问题:
(1)1辆A型车和1辆车B型车都载满货物一次可分别运货多少吨?
(2)请你帮该物流公司设计租车方案;
(3)若A型车每辆需租金100元/次,B型车每辆需租金120元/次.请选出最省钱的租车方案,并求出最少租车费.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数y=ax2+bx+c(a>0)图象的顶点为D,其图象与x轴的交点A、B的横坐标分别为﹣1,3.与y轴负半轴交于点C,在下面五个结论中:
①2a﹣b=0;②a+b+c>0;③c=﹣3a;④只有当a=
 时,△ABD是等腰直角三角形;⑤使△ACB为等腰三角形的a值可以有四个.
时,△ABD是等腰直角三角形;⑤使△ACB为等腰三角形的a值可以有四个.其中正确的结论是 .(只填序号)

-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场第一次用10000元购进甲、乙两种商品,销售完成后共获利2200元,其中甲种商品每件进价60元,售价70元;乙种商品每件进价50元,售价65元.
(1)求该商场购进甲、乙两种商品各多少件?
(2)商场第二次以原进价购进甲、乙两种商品,且购进甲、乙商品的数量分别与第一次相同,甲种商品按原售价出售,而乙种商品降价销售,要使第二次购进的两种商品全部售出后,获利不少于1800元,乙种商品最多可以降价多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】等式(x+6)0=1成立的条件是( )
A. x为有理数 B. x≠0 C. x≠6 D. x≠﹣6
相关试题

