【题目】如图,己知△ABC中,AB=3,AC=4,BC=5,作∠ABC的角平分线交AC于D,以D为圆心,DA为半径作圆,与射线交于点E、F.有下列结论: ①△ABC是直角三角形;②⊙D与直线BC相切;③点E是线段BF的黄金分割点;④tan∠CDF=2.
其中正确的结论有( )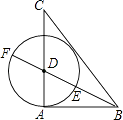
A.4个
B.3个
C.2个
D.1个
参考答案:
【答案】A
【解析】解:∵32+42=52 , ∴AB2+AC2=AB2 ,
∴△ABC是直角三角形,∠BAC=90°,①正确;
作DM⊥BC于M,如图所示:
∵BD是∠ABC的平分线,
∴DM=DA,
∴⊙D与直线BC相切,
∴②正确;
∵∠BAC=∠DMC=90°,
在Rt△BDM和△BDA中,![]() ,
,
∴Rt△BDM≌△BDA(HL),
∴MB=AB=3,
∴CM=BC﹣MB=2,
∵∠C=∠C,
∴△CDM∽△CBA,
∴ ![]() ,即
,即 ![]() ,
,
解得:DM= ![]() ,
,
∴DF=DE= ![]() ,
,
∴BD= ![]() =
= ![]() =
= ![]() ,
,
∴BE=BD﹣DE= ![]() ﹣
﹣ ![]() ,BF=BD+DF=
,BF=BD+DF= ![]() +
+ ![]() ,
,
∵EF2=9,BFBE=( ![]() +
+ ![]() )(
)( ![]() ﹣
﹣ ![]() )=9,
)=9,
∴EF2=BFBE,
∴点E是线段BF的黄金分割点,③正确;
∵tan∠CDF=tan∠ADB= ![]() =
= ![]() =2,
=2,
∴④正确;
正确的有4个.
故选:A.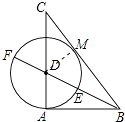
【考点精析】通过灵活运用切线的判定定理和黄金分割,掌握切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线;把线段AB分成两条线段AC,BC(AC>BC),并且使AC是AB和BC的比例中项,叫做把线段AB黄金分割,点C叫做线段AB的黄金分割点,其中AC=0.618AB即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某检修小组乘坐一辆汽车沿东西方向的公路检修输电线路,规定向东为正,他们从A地出发到收工时,走过的路程记录如下:(单位:千米)
 ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  .
.(1)他们收工时距A地多远?
(2)他们离出发点A最远时有多远?
(3)汽车每千米耗油
 升,从出发到返回A地共耗油多少升?
升,从出发到返回A地共耗油多少升? -
科目: 来源: 题型:
查看答案和解析>>【题目】(2017辽宁省盘锦市,第18题,3分)如图,点A1(1,1)在直线y=x上,过点A1分别作y轴、x轴的平行线交直线
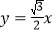 于点B1,B2,过点B2作y轴的平行线交直线y=x于点A2,过点A2作x轴的平行线交直线
于点B1,B2,过点B2作y轴的平行线交直线y=x于点A2,过点A2作x轴的平行线交直线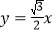 于点B3,…,按照此规律进行下去,则点An的横坐标为______.
于点B3,…,按照此规律进行下去,则点An的横坐标为______.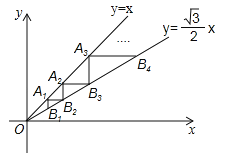
-
科目: 来源: 题型:
查看答案和解析>>【题目】(背景)某班在一次数学实践活动中,对矩形纸片进行折叠实践操作,并将其产生的数学问题进行相关探究. (操作)如图,在矩形ABCD中,AD=6,AB=4,点P是BC边上一点,现将△APB沿AP对折,得△APM,显然点M位置随P点位置变化而发生改变
(问题)试求下列几种情况下:点M到直线CD的距离
(1)∠APB=75°;
(2)P与C重合;
(3)P是BC的中点. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长为3cm,动点P从B点出发以3cm/s的速度沿着边BC﹣CD﹣DA运动,到达A点停止运动;另一动点Q同时从B点出发,以1cm/s的速度沿着边BA向A点运动,到达A点停止运动.设P点运动时间为x(s),△BPQ的面积为y(cm2),则y关于x的函数图象是( )
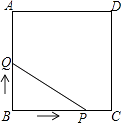
A.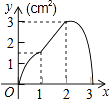
B.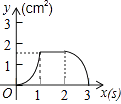
C.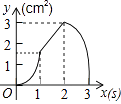
D.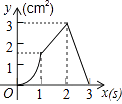
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知代数式A=x2+3xy+x-
 ,B=2x2-xy+4y-1
,B=2x2-xy+4y-1(1)当x=y=-2时,求2A-B的值;
(2)若2A-B的值与y的取值无关,求x的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市雾霾天气趋于严重,甲商场根据民众健康需要,代理销售每台进价分别为600元、560
元的 A、B 两种型号的空气净化器,如表是近两周的销售情况:(进价、售价均保持不变,利润=销
售收入进货成本)
销售时段
销售数量
销售收入
(元)
A种型号
(台)
B种型号
(台)
第一周
3
2
3960
第二周
5
4
7120
(1)求 A,B 两种型号的空气净化器的销售单价;
(2)该商店计划一次购进两种型号的空气净化器共30台,其中B型净化器的进货量不超过A型的2倍.设购进A型空气净化器为x台,这30台空气净化器的销售总利润为y元.
①请写出y关于x的函数关系式;
②该商店购进A型、B型净化器各多少台,才能使销售总利润最大?
相关试题

