【题目】如图,将矩形纸片ABCD(图1)按如下步骤操作:(1)以过点A的直线为折痕
折叠纸片,使点B恰好落在AD边上,折痕与BC边交于点E(如图2);(2)以过点E的
直线为折痕折叠纸片,使点A落在BC边上,折痕EF交AD边于点F(如图3);(3)将纸
片收展平,那么∠AFE的度数为 ( )

A. 60° B. 67.5° C. 72° D. 75°
参考答案:
【答案】B
【解析】
折叠是一种对称变换,它属于轴对称,根据轴对称的性质,可利用角度的关系求解.
解:第一次折叠后,∠EAD=45°,∠AEC=135°;
第二次折叠后,∠AEF=67.5°,∠FAE=45°;
故由三角形内角和定理知,∠AFE=67.5度.
故选B.
本题考查图形的折叠变化及三角形的内角和定理.
关键是要理解折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,只是位置变化.
-
科目: 来源: 题型:
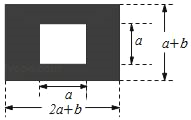
查看答案和解析>>【题目】如图,某市有一块长为(2a+b)米,宽为(a+b)米的长方形地块,规划部门计划将阴影部分进行绿化,中间将修建一座雕像.
(1)试用含a,b的代数式表示绿化的面积是多少平方米?
(2)若a=3,b=2,请求出绿化面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】图a是一个长为2m、宽为2n的长方形,沿图中实现用剪刀均分成四块小长方形,然后按图b的形状拼成一个正方形.

(1)图b中,大正方形的边长是 .阴影部分小正方形的边长是 ;
(2)观察图b,写出(m+n)2,(m﹣n)2,mn之间的一个等量关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个正整数能表示成两个连续偶数的平方差,那么这个正整数为“神秘数”.
如:


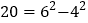
因此,4,12,20这三个数都是神秘数.
(1)28和2012这两个数是不是神秘数?为什么?
(2)设两个连续偶数为
 和
和 (其中
(其中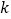 为非负整数),由这两个连续偶数构造的神秘数是4的倍数,请说明理由.
为非负整数),由这两个连续偶数构造的神秘数是4的倍数,请说明理由. (3)两个连续奇数的平方差(取正数)是不是神秘数?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(3分)如图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2BF.给出下列四个结论:①DE=DF;②DB=DC;③AD⊥BC;④AC=3BF,其中正确的结论共有( )

A. 4个 B. 3个 C. 2个 D. 1个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知:∠BAC的平分线与BC的垂直平分线DG相交于点D,DE⊥AB,DF⊥AC,垂足分别为E、F,AB=6,AC=3,则BE=_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】海静中学开展以“我最喜爱的职业”为主题的调查活动,围绕“在演员、教师、医生、律师、公务员共五类职业中,你最喜爱哪一类?(必选且只选一类)”的问题,在全校范围内随机抽取部分学生进行问卷调查,将调查结果整理后绘制成如图所示的不完整的统计图,请你根据图中提供的信息回答下列问题:
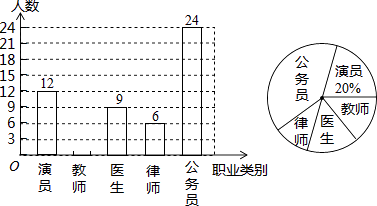
(1)本次调查共抽取了多少名学生?
(2)求在被调查的学生中,最喜爱教师职业的人数,并补全条形统计图;
(3)若海静中学共有1500名学生,请你估计该中学最喜爱律师职业的学生有多少名?
相关试题

