【题目】![]() 、
、![]() 两仓库分别有水泥
两仓库分别有水泥![]() 吨和
吨和![]() 吨,
吨,![]() 、
、![]() 两工地分别需要水泥
两工地分别需要水泥![]() 吨和
吨和![]() 吨.已知从
吨.已知从![]() 、
、![]() 仓库到
仓库到![]() 、
、![]() 工地的运价如下表:
工地的运价如下表:
到 | 到 | |
| 每吨 | 每吨 |
| 每吨 | 每吨 |
1)若从![]() 仓库运到
仓库运到![]() 工地的水泥为
工地的水泥为![]() 吨,则用含
吨,则用含![]() 的代数式表示从
的代数式表示从![]() 仓库运到
仓库运到![]() 工地的水泥为_____吨,从
工地的水泥为_____吨,从![]() 仓库将水泥运到
仓库将水泥运到![]() 工地的运输费用为______元;
工地的运输费用为______元;
(2)求把全部水泥从![]() 、
、![]() 两仓库运到
两仓库运到![]() 、
、![]() 两工地的总运输费(用含
两工地的总运输费(用含![]() 的代数式表示并化简);
的代数式表示并化简);
(3)如果从![]() 仓库运到
仓库运到![]() 工地的水泥为
工地的水泥为![]() 吨时,那么总运输费为多少元?
吨时,那么总运输费为多少元?
参考答案:
【答案】(1)(20-x),(9x+135);(2)(2x+525);(3)545元.
【解析】
(1)![]() 仓库原有的20吨减去运到
仓库原有的20吨减去运到![]() 工地的水泥,就是运到
工地的水泥,就是运到![]() 工地的水泥;首先求出
工地的水泥;首先求出![]() 仓库运到
仓库运到![]() 仓库的吨数,也就是
仓库的吨数,也就是![]() 工地需要的水泥减去从
工地需要的水泥减去从![]() 仓库运到
仓库运到![]() 工地的水泥,然后用
工地的水泥,然后用![]() 仓库运到
仓库运到![]() 仓库的吨数再乘每吨的运费即可;
仓库的吨数再乘每吨的运费即可;
(2)用![]() 表示出
表示出![]() 、
、![]() 两个仓库分别向
两个仓库分别向![]() 、
、![]() 运送的吨数,再乘每吨的运费,然后合并起来即可;
运送的吨数,再乘每吨的运费,然后合并起来即可;
(3)把![]() 代入(2)中的代数式,求得问题的解.
代入(2)中的代数式,求得问题的解.
解:(1)根据题意列表如下:
到 | 到 | |
| x | 20-x |
| 15-x | 35-(20-x)=15+x |
从A地运到D地的水泥为:(20-x),
从B地将水泥运到D地的运输费用为:9[35-(20-x)]=9x+135;
故答案为:(20-x),(9x+135);
(2)总运输费:15x+12(20-x)+10(15-x)+9[35-(20-x)]=(2x+525)元;
(3)当![]() 时,2x+525=2×10+525=545(元)
时,2x+525=2×10+525=545(元)
答:总运费为545元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点C是以AB为直径的⊙O上一动点,过点C作⊙O直径CD,过点B作BE⊥CD于点E.已知AB=6cm,设弦AC的长为xcm,B,E两点间的距离为ycm(当点C与点A或点B重合时,y的值为0).
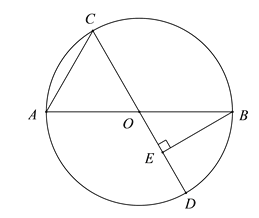
小冬根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.
下面是小冬的探究过程,请补充完整:
(1)通过取点、画图、测量,得到了x与y的几组值,如下表:
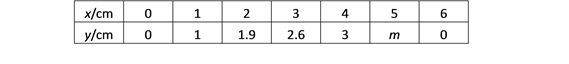
经测量m的值是(保留一位小数).
(2)建立平面直角坐标系,描出表格中所有各对对应值为坐标的点,画出该函数的图象;

(3)在(2)的条件下,当函数图象与直线
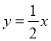 相交时(原点除外),∠BAC的度数是_____.
相交时(原点除外),∠BAC的度数是_____. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把矩形OABC放入平面直角坐标系xO中,使OA、OC分别落在x、y轴的正半轴上,其中AB=15,对角线AC所在直线解析式为y=﹣
 x+b,将矩形OABC沿着BE折叠,使点A落在边OC上的点D处.
x+b,将矩形OABC沿着BE折叠,使点A落在边OC上的点D处.(1)求点B的坐标;
(2)求EA的长度;
(3)点P是y轴上一动点,是否存在点P使得△PBE的周长最小,若存在,请求出点P的坐标,若不存在,请说明理由.

-
科目: 来源: 题型:
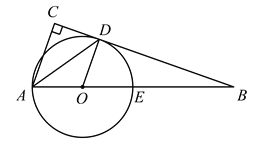
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,AD平分∠BAC交BC于点D,点O是AB边上一点,以O为圆心作⊙O且经过A,D两点,交AB于点E.
(1)求证:BC是⊙O的切线;
(2)AC=2,AB=6,求BE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某天早晨,王老师从家出发步行前往学校,途中在路边一饭店吃早餐,如图所示是王老师从家到学校这一过程中的所走路程s(米)与时间t(分)之间的关系.
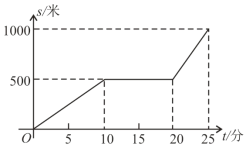
(1)学校离他家 米,从出发到学校,王老师共用了 分钟;王老师吃早餐用了 分钟?
(2)观察图形直接回答王老师吃早餐以前的速度快还是吃完早餐以后的速度快?
(3)求出王老师吃完早餐后的平均速度是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】我国古代数学著作《九章算术》中的一个问题.原文是:今有池方一丈,葭生其中央,出水尺.引葭赴岸,适与岸齐问水深、葭长各几何译文大意是:如图,有一个水池,水面是一个边长为10尺的正方形,在水池正中央有一根芦苇,它高出水面1尺.如果把这根芦苇拉向水池边的中点,它的顶端恰好到达池边的水面.问水的深度与这根芦苇的长度分别是多少?

-
科目: 来源: 题型:
查看答案和解析>>【题目】根据要求作图.
(1)如图1,平行四边形ABCD,点E,F分别在边AD,BC上,且AE=CF,连接EF.请你只用无刻度直尺画出线段EF的中点O.(保留画图痕迹,不必说明理由).
(2)如图2,平行四边形ABCD,点E在边AB上,请你只用无刻度直尺在边CD上找一点F,使得四边形AECF为平行四边形,并说明理由.(注意:无刻度直尺只能过点画线段或直线或射线).

相关试题

