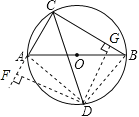
【题目】如图,圆O的直径AB为13cm,弦AC为5cm,∠ACB的平分线圆O于D,则CD长是_______cm

参考答案:
【答案】![]()
【解析】试题分析:首先作DF⊥CA,交CA的延长线于点F,作DG⊥CB于点G,连接DA,DB.由CD平分∠ACB,根据角平分线的性质得出DF=DG,由HL证明△AFD≌△BGD,得出CF的长,又△CDF是等腰直角三角形,从而求出CD的长.
解:作DF⊥CA,垂足F在CA的延长线上,作DG⊥CB于点G,连接DA,DB.
∵CD平分∠ACB,
∴∠ACD=∠BCD
∴DF=DG,![]() ,
,
∴DA=DB.
∵∠AFD=∠BGD=90°,
在Rt△ADF和Rt△BDG,
![]() ,
,
∴Rt△AFD≌Rt△BGD(HL),
∴AF=BG.
同理:Rt△CDF≌Rt△CDG(HL),
∴CF=CG.
∵AB是直径,
∴∠ACB=90°,
∵AC=5cm,AB=13cm,
∴BC=![]() =12(cm),
=12(cm),
∴5+AF=12﹣AF,
∴AF=![]() ,
,
∴CF=![]() ,
,
∵CD平分∠ACB,
∴∠ACD=45°,
∵△CDF是等腰直角三角形,
∴CD=![]() (cm).
(cm).
故答案为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二元一次方程3x-y=1,当x=2时,y等于( )
A.5 B.-3 C.-7 D.7
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,∠ABC和∠ACB的平分线交于点O,过点O作EF∥BC,交AB,AC于点E,F.
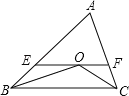
(1)若∠ABC=50°,∠ACB=60°,求∠BOC的度数;
(2)若∠BEF+∠CFE=a,求∠BOC的度数.(用含a的代数式表示)
-
科目: 来源: 题型:
查看答案和解析>>【题目】将一矩形纸片OABC放在平面直角坐标系中,O(0,0),A(6,0),C(0,3).动点Q从点O出发以每秒1个单位长的速度沿OC向终点C运动,运动
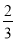 秒时,动点P从点A出发以相等的速度沿AO向终点O运动.当其中一点到达终点时,另一点也停止运动.设点P的运动时间为t(秒).
秒时,动点P从点A出发以相等的速度沿AO向终点O运动.当其中一点到达终点时,另一点也停止运动.设点P的运动时间为t(秒).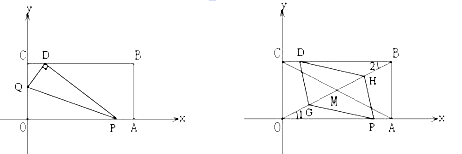
(1)求点B的坐标,并用含t的代数式表示OP,OQ;
(2)当t=1时,如图1,将△OPQ沿PQ翻折,点O恰好落在CB边上的点D处,求点D的坐标;
(3)在(2)的条件下,矩形对角线AC,BO交于M,取OM中点G,BM中点H,求证当t=1时四边形DGPH是平行四边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x-2y=6,x-3y=4,则x2-5xy+6y2的值为______ .
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.a2+a3=a5
B.a2a3=a6
C.(a2b3)3=a5b6
D.(a2)3=a6 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知点(﹣2,y1),(﹣1,y2),(1,y3)都在直线y=﹣3x+2上,则y1,y2,y3的值的大小关系是( )
A. y3<y1<y2 B. y1<y2<y3 C. y3>y1>y2 D. y1>y2>y3
相关试题

