【题目】如图,在△ABC中,AB=AC,AD平分∠BAC,O是AC的中点,连接DO,过点C作CE∥DA,交DO的延长线于点E,连接AE.

(1)求证:四边形ADCE是矩形;
(2)若F是CE上的动点(点F不与C、E重合),连接AF、DF、BE,请直接写出图2中与四边形ABDF面积相等的所有的三角形和四边形(四边形ABDF除外)
参考答案:
【答案】(1)详见解析;(2)S四边形ABDF=S四边形ABDE.
【解析】
试题分析:(1)根据全等三角形的判定求出△ADO≌△CEO,求出OD=OE,根据平行四边形的判定得出四边形ADCE是平行四边形,再根据矩形的判定得出即可;(2)根据面积公式和等底等高的三角形的面积相等得出即可.
试题解析:(1)证明:∵CE∥DA,
∴∠OCE=∠OAD,
∵O为AC的中点,
∴OA=OC,
在△ADO和△CEO中
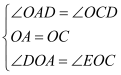
∴△ADO≌△CEO(ASA),
∴OD=OE,
∵OA=OC,
∴四边形ADCE是平行四边形,
∵AB=AC,AD平分∠BAC,
∴AD⊥BC,
∴∠ADC=90°,
∴平行四边形ADCE是矩形;
(2)解:图2中与四边形ABDF面积相等的所有的三角形和四边形有△ABC,△BCE,矩形ADCE,四边形ABDE,
理由是:∵△ACD和△AFD的面积相等(等底等高的三角形面积相等),
∴S△ADC=S△ADF,
∴S△ADC+S△ADB=S△ADF+S△ADB,
∴S四边形ABDF=S△ABC;
∵S△BCE=S△ABC,
∴S四边形ABDF=S△BCE;
∵S△ADB=S△ADC,S△ADF=S△AEC,
∴S四边形ABDF=S矩形ADCE;
∵S△ADF=S△ADE,
∴都加上△ADB的面积得:S四边形ABDF=S四边形ABDE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若x2﹣kxy+9y2是一个完全平方式,则k的值为( )
A. 3 B. ±6 C. 6 D. +3
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算下列各题
(1)5+(﹣6)﹣(﹣2)
(2)|﹣4|﹣12×( ﹣
﹣  )
)
(3)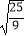 +(﹣
+(﹣  )2÷(﹣
)2÷(﹣  )
)
(4)2×(﹣1)2012+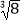 ÷(﹣
÷(﹣  )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,这是由8个同样大小的立方体组成的魔方,体积为64.
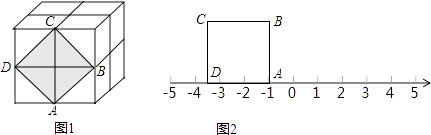
(1)求出这个魔方的棱长.
(2)图中阴影部分是一个正方形ABCD,求出阴影部分的面积及其边长.
(3)把正方形ABCD放到数轴上,如图2,使得A与﹣1重合,那么D在数轴上表示的数为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】若|a|=﹣a,则a为( )
A. a是负数 B. a是正数 C. a=0 D. 负数或零
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式中,不相等的是( )
A. (﹣2)2和22 B. |﹣2|3和|﹣23|
C. (﹣2)2和﹣22 D. (﹣2)3和﹣23
-
科目: 来源: 题型:
查看答案和解析>>【题目】某人去水果批发市场采购苹果,他看中了A、B两家苹果.这两家苹果品质一样,零售价都为6元/千克,批发价各不相同.A家规定:批发数量不超过1000千克,按零售价的92%优惠;批发数量不超过2000千克,按零售价的90%优惠;超过2000千克的按零售价的88%优惠.B家的规定如下表:
数量范围(千克)
0~500
500以上~1500
1500以上~2500
2500以上
价 格(元)
零售价的95%
零售价的85%
零售价的75%
零售价的70%
[表格说明:批发价格分段计算,如:某人批发苹果2100千克,则总费用=6×95%×500+6×85%×1000+6×75%×(2100﹣1500)]
(1)如果他批发600千克苹果,则他在A 家批发需要元,在B家批发需要元;
(2)如果他批发x千克苹果(1500<x<2000),则他在A 家批发需要元,在B家批发需要元(用含x的代数式表示);
(3)现在他要批发1800千克苹果,你能帮助他选择在哪家批发更优惠吗?请说明理由.
相关试题

