【题目】我们常见的炒菜锅和锅盖都是抛物面,经过锅心和盖心的纵断面是由两段抛物线组合而成的封闭图形,不妨简称为“锅线”.锅口直径为6dm,锅深3dm,锅盖高1dm(锅口直径与锅盖直径视为相同),建立直角坐标系如图1所示,如果把锅纵断面的抛物线记为C1 , 把锅盖纵断面的抛物线记为C2 . 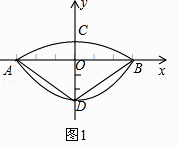
(1)求C1和C2的解析式;
(2)如图2,过点B作直线BE:y= ![]() x﹣1交C1于点E(﹣2,﹣
x﹣1交C1于点E(﹣2,﹣ ![]() ),连接OE、BC,在x轴上求一点P,使以点P、B、C为顶点的△PBC与△BOE相似,求出P点的坐标;
),连接OE、BC,在x轴上求一点P,使以点P、B、C为顶点的△PBC与△BOE相似,求出P点的坐标;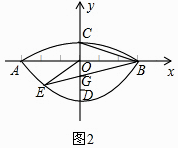
(3)如果(2)中的直线BE保持不变,抛物线C1或C2上是否存在一点Q,使得△EBQ的面积最大?若存在,求出Q的坐标和△EBQ面积的最大值;若不存在,请说明理由.
参考答案:
【答案】
(1)
解:由题意A(﹣3,0),B(3,0),C(0,1),D(0,﹣3)
设抛物线记为C2的解析式为y=ax2+c,
把B(3,0),C(0,﹣1)代入得到 ![]() ,解得
,解得 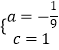 ,
,
∴抛物线记为C2的解析式为y=﹣ ![]() x2+1,
x2+1,
同法可得抛物线记为C1的解析式为y= ![]() x2﹣3
x2﹣3
(2)
解:∵y= ![]() x﹣1交C1于点E(﹣2,﹣
x﹣1交C1于点E(﹣2,﹣ ![]() ),
),
∴BE= ![]() =
= ![]() ,
,
设直线BE与y轴的交点为F,
由y= ![]() x﹣1,可得F(0,﹣1),
x﹣1,可得F(0,﹣1),
∵OF=OC=1,OB=OB,∠BOC=∠BOF,
∴△BOC≌△BOF,
∴∠OBC=∠EOB,
因此可能存在两种情形,设P(x,0),
①当△PBC∽△OBE时, ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,解得x=
,解得x= ![]() ,
,
∴点P坐标为( ![]() ,0).
,0).
②当△PBC∽△EBO时, ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,解得x=﹣
,解得x=﹣ ![]() ,
,
∴点P坐标为(﹣ ![]() ,0).
,0).
③∵∠OBC≠∠AOE,
∴不存在点P在点B右侧的情形,
综上所述,满足条件的点P坐标( ![]() ,0)或(﹣
,0)或(﹣ ![]() ,0)
,0)
(3)
解:要使△EBQ的面积最大,则点Q到直线BE的距离最大时,过点Q的直线与直线BE平行,且与抛物线只有一个交点.
①如图1中,当点Q在C1上时,
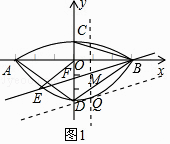
设与抛物线只有一个交点的直线为y= ![]() x+b,则点Q(x,
x+b,则点Q(x, ![]() x+b),代入y=
x+b),代入y= ![]() x2﹣3,得到
x2﹣3,得到 ![]() x2﹣3=
x2﹣3= ![]() x+b,整理得x2﹣x﹣9﹣3b=0,
x+b,整理得x2﹣x﹣9﹣3b=0,
∵△=0,
∴1﹣4(﹣9﹣3b)=0,
∴b=﹣ ![]() ,
,
∴y= ![]() x﹣
x﹣ ![]() ,
,
由 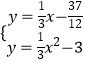 ,解得
,解得 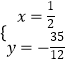 ,
,
∴Q( ![]() ,﹣
,﹣ ![]() ),
),
过Q作x轴的垂线交直线BE于M,
把x= ![]() 代入y=
代入y= ![]() x﹣1,可得M(
x﹣1,可得M( ![]() ,﹣
,﹣ ![]() ),
),
∴MQ=﹣ ![]() ﹣(﹣
﹣(﹣ ![]() )=
)= ![]() ,
,
∴△EBQ面积的最大值为 ![]() ×
× ![]() ×(2+3)=
×(2+3)= ![]() .
.
②如图2中,当Q在C2上时,
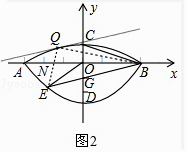
设与抛物线只有一个交点的直线为y= ![]() x+b′,则Q(x,
x+b′,则Q(x, ![]() x+b′),代入y=﹣
x+b′),代入y=﹣ ![]() x2+1,可得x2+3x﹣9+9b′=0,
x2+1,可得x2+3x﹣9+9b′=0,
∵△=0,
∴9﹣4(9b′﹣9)=0,
∴b′= ![]() ,
,
∴y= ![]() x+
x+ ![]() ,与y=﹣
,与y=﹣ ![]() x2+1联列方程组,解得Q(﹣
x2+1联列方程组,解得Q(﹣ ![]() ,
, ![]() ),连接EQ,交x轴于N.
),连接EQ,交x轴于N.
易知直线QE的解析式为y= ![]() x+8,
x+8,
∴N(﹣ ![]() ,0),
,0),
∴BN=3﹣(﹣ ![]() )=
)= ![]() ,
,
∴△QEB的面积最大值为 ![]() ×
× ![]() ×[
×[ ![]() ﹣(﹣
﹣(﹣ ![]() )]=
)]= ![]() =
= ![]() ,
,
∵ ![]() >
> ![]() ,
,
∴△EBQ的面积的最大值为 ![]() ,此时Q(﹣
,此时Q(﹣ ![]() ,
, ![]() ).
).
【解析】(1)根据题意确定A、B、C、D的坐标,利用待定系数法即可解决问题;(2)首先证明∠OBC=∠EOB,因此可能存在两种情形,设P(x,0),①当△PBC∽△OBE时,②当△PBC∽△EBO时,分别求解即可.(3)要使△EBQ的面积最大,则点Q到直线BE的距离最大时,过点Q的直线与直线BE平行,且与抛物线只有一个交点.①如图1中,当点Q在C1上时,设与抛物线只有一个交点的直线为y= ![]() x+b,则点Q(x,
x+b,则点Q(x, ![]() x+b),代入y=
x+b),代入y= ![]() x2﹣3,得到
x2﹣3,得到 ![]() x2﹣3=
x2﹣3= ![]() x+b,整理得x2﹣x﹣9﹣3b=0,由△=0,可得1﹣4(﹣9﹣3b)=0,推出b=﹣
x+b,整理得x2﹣x﹣9﹣3b=0,由△=0,可得1﹣4(﹣9﹣3b)=0,推出b=﹣ ![]() ,可得y=
,可得y= ![]() x﹣
x﹣ ![]() ,由
,由 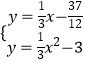 ,求出Q的坐标即可解决问题.②如图2中,当Q在C2上时,同法可求.
,求出Q的坐标即可解决问题.②如图2中,当Q在C2上时,同法可求.
-
科目: 来源: 题型:
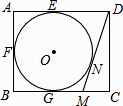
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=4,AD=5,AD、AB、BC分别与⊙O相切于E、F、G三点,过点D作⊙O的切线交BC于点M,切点为N,则DM的长为( )
A.
B.2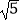
C.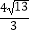
D.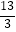
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABO中,斜边AB=1.若OC//BA,∠AOC=36°,则( )

A.点B到AO的距离为sin54°
B.点B到AO的距离为tan36°
C.点A到OC的距离为sin36°sin54°
D.点A到OC的距离为cos36°sin54° -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=﹣3x+3与x轴交于点B,与y轴交于点A,以线段AB为边,在第一象限内作正方形ABCD,点C落在双曲线y=
 (k≠0)上,将正方形ABCD沿x轴负方向平移a个单位长度,使点D恰好落在双曲线y=
(k≠0)上,将正方形ABCD沿x轴负方向平移a个单位长度,使点D恰好落在双曲线y=  (k≠0)上的点D1处,则a= .
(k≠0)上的点D1处,则a= . 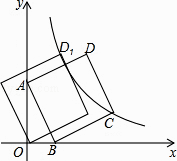
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直角梯形ABCD中,AB//DC,∠DAB=90°,AD=2DC=4,AB=6.动点M以每秒1个单位长的速度,从点A沿线段AB向点B运动;同时点P以相同的速度,从点C沿折线C﹣D﹣A向点A运动.当点M到达点B时,两点同时停止运动.过点M作直线l//AD,与线段CD的交点为E,与折线A﹣C﹣B的交点为Q.点M运动的时间为t(秒).
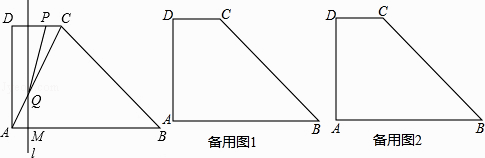
(1)当t=0.5时,求线段QM的长;
(2)当0<t<2时,如果以C、P、Q为顶点的三角形为直角三角形,求t的值;
(3)当t>2时,连接PQ交线段AC于点R.请探究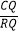 是否为定值,若是,试求这个定值;若不是,请说明理由.
是否为定值,若是,试求这个定值;若不是,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】现在,苏宁商场进行促销活动,出售一种优惠购物卡(注:此卡只作为购物优惠凭证不能顶替货款),花300元买这种卡后,凭卡可在这家商场按标价的8折购物.
(1)顾客购买多少元金额的商品时,买卡与不买卡花钱相等?在什么情况下购物合算?
(2)小张要买一台标价为3500元的冰箱,如何购买合算?小张能节省多少元钱?
(3)小张按合算的方案,把这台冰箱买下,如果商场还能盈利25%,这台冰箱的进价是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】探索性问题:
已知:b是最小的正整数,且a、b满足(c﹣5)2+|a+b|=0,请回答问题:
(1)请直接写出a、b、c的值.a= ,b= ,c= ;
(2)数轴上a、b、c三个数所对应的点分别为A、B、C,点A、B、C同时开始在数轴上运动,若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒1个单位长度和3个单位长度的速度向右运动,假设t秒钟过后,若点B与点C之间的距离表示为BC,点A与点B之间的距离表示为AB,点A与点C之间的距离表示为AC.
①t秒钟过后,AC的长度为 (用t的关系式表示);
②请问:BC﹣AB的值是否随着时间t的变化而改变?若变化,请说明理由;若不变,请求其值.

相关试题

