【题目】如图,在等腰三角形ABC中,AB=AC,∠BAC=50°.∠BAC的平分线与AB的中垂线相交于点O,点C沿EF折叠后与点O重合,求∠CEF的度数.

参考答案:
【答案】50°
【解析】试题分析:连接OB,根据中垂线的性质就可以得出AO=BO,就有∠OAB=∠OBA,根据角平分线的性质就可以求出∠EBO的度数,通过△ABO≌△ACO就有BO=CO,就有∠OBC=∠OCB,再由轴对称就可以求出OE=CE,从而求出结论.
试题解析:连接OB,
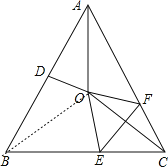
∵OD垂直平分AB,
∴AO=BO,
∴∠OAB=∠OBA.
∵AB=AC,∠BAC=50°,
∴∠ABC=∠ACB=65°.
∵OA平分∠BAC,
∴∠BAO=∠CAO=![]() ∠BAC=25°,
∠BAC=25°,
∴∠OBA=25°,
∴∠OBC=40°.
在△ABO和△ACO中
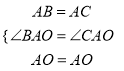 ,
,
∴△ABO≌△ACO(SAS),
∴BO=CO,
∴∠OBC=∠OCB=40°.
∵△EOF与△ECF关于EF对称,
∴△EOF≌△ECF,
∴OE=CE,∠OEF=∠CEF=![]() ∠OEC..
∠OEC..
∴∠ECO=∠EOC=40°,
∴∠OEC=100°,
∴∠CEF=50°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a<b,则下列不等式中不正确的是( )
A. 4a<4b B. a+4<b+4 C. a﹣4<b﹣4 D. ﹣4a<﹣4b
-
科目: 来源: 题型:
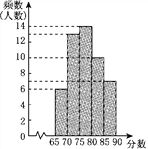
查看答案和解析>>【题目】某市招聘教师,对应聘者分别进行教学能力、科研能力、组织能力三项测试,其中甲、乙两人的成绩如下表:(单位:分)

(1)根据实际需要,将教学能力、科研能力、组织能力三项测试得分按5∶3∶2的比确定最后成绩,若按此成绩在甲、乙两人中录用一人,谁将被录用?
(2)按照(1)中的成绩计算方法,将每位应聘者的最后成绩绘制成如图所示的频数分布直方图(每组分数段均包含左端数值,不包含右端数值),并决定由高分到低分录用8人.甲、乙两人能否被录用?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2016年G20峰会将于9月4﹣5日在杭州举行,“丝绸细节”助力杭州打动世界,某丝绸公司为G20设计手工礼品.投入W元钱,若以2条领带和1条丝巾为一份礼品,则刚好可制作600份礼品;若以1条领带和3条丝巾为一份礼品,则刚好可制作400份奖品.
(1)若W=24万元,求领带及丝巾的制作成本各是多少?
(2)若用W元钱全部用于制作领带,总共可以制作几条?
(3)若用W元钱恰好能制作300份其他的礼品,可以选择a条领带和b条丝巾作为一份礼品(两种都要有),请求出所有可能的a、b值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,BD∥GE,AQ平分∠FAC,交BD于Q,∠GFA=50°,∠Q=25°,则∠ACB的度数( )
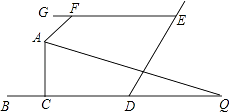
A.90°
B.95°
C.100°
D.105° -
科目: 来源: 题型:
查看答案和解析>>【题目】 下列事件中,属于必然事件的是( )
A. “世界杯新秀”姆巴佩发点球 100%进球
B. 任意购买一张车票,座位刚好挨着窗口
C. 三角形内角和为 180°
D. 叙利亚不会发生战争
-
科目: 来源: 题型:
查看答案和解析>>【题目】我国南宋时期杰出的数学家杨辉是钱塘人,如图是他在《详解九章算术》中记载的“杨辉三角”.此图揭示了(a+b)n(n为非负整数)的展开式的项数及各项系数的有关规律.
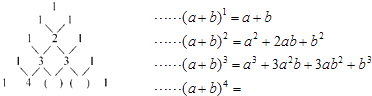
(1)请仔细观察,填出(a+b)4的展开式中所缺的系数.(a+b)4=a4+4a3b+a2b2+ab2+b4
(2)此规律还可以解决实际问题:假如今天是星期三,再过7天还是星期三,那么再过814天是星期 .
相关试题

