Question

【题目】在矩形ABCD中，AB=6cm，BC=12cm，点P从点A出发，沿AB边向点B以每秒1cm的速度移动，同时点Q从点B出发沿BC边向点C以每秒2cm的速度移动P、Q两点在分别到达B、C两点后就停止移动，设两点移动的时间为t秒，回答下列问题：

（1）如图1，当t为几秒时，△PBQ的面积等于5cm2？

（2）如图2，当t=秒时，试判断△DPQ的形状，并说明理由；

（3）如图3，以Q为圆心，PQ为半径作⊙Q．

①在运动过程中，是否存在这样的t值，使⊙Q正好与四边形DPQC的一边（或边所在的直线）相切？若存在，求出t值；若不存在，请说明理由；

②若⊙Q与四边形DPQC有三个公共点，请直接写出t的取值范围。

Answer 1

【答案】（1）1秒或5秒（2）直角三角形（3）①t=0或t=﹣18+12②0＜t＜6﹣18

【解析】试题分析：（1）由题意可知PA=t，BQ=2t，从而得到PB=6﹣t，BQ=2t，然后根据△PQB的面积=5cm2列方程求解即可；

（2）由t=，可求得AP=，QB=3，PB=，CQ=9，由勾股定理可证明DQ2+PQ2=PD2，由勾股定理的逆定理可知△DPQ为直角三角形；

（3）①当t=0时，点P与点A重合时，点B与点Q重合，此时圆Q与PD相切；当⊙Q正好与四边形DPQC的DC边相切时，由圆的性质可知QC=QP，然后依据勾股定理列方程求解即可；

②先求得⊙Q与四边形DPQC有两个公共点时t的值，然后可确定出t的取值范围．

试题解析：（1）∵当运动时间为t秒时，PA=t，BQ=2t，

∴PB=6﹣t，BQ=2t．

∵△PBQ的面积等于5cm2，

∴PBBQ=（6﹣t）2t．

∴．

解得：t1=1，t2=5．

答：当t为1秒或5秒时，△PBQ的面积等于5cm2．

（2）△DPQ的形状是直角三角形．

理由：∵当t=秒时，AP=，QB=3，

∴PB=6﹣=，CQ=12﹣3=9．

在Rt△PDA中，由勾股定理可知：PD2=DA2+PA2=122+（）2=．

同理：在Rt△PBQ和Rt△DCQ中由勾股定理可得：DQ2=117，PQ2=．

∵117+=，

∴DQ2+PQ2=PD2．

所以△DPQ的形状是直角三角形．

（3span>）①（Ⅰ）由题意可知圆Q与AB、BC不相切．

（Ⅱ）如图1所示：当t=0时，点P与点A重合时，点B与点Q重合．

∵∠DAB=90°，

∴∠DPQ=90°．

∴DP⊥PQ．

∴DP为圆Q的切线．

（Ⅲ）当⊙Q正好与四边形DPQC的DC边相切时，如图2所示．

由题意可知：PB=6﹣t，BQ=2t，PQ=CQ=12﹣2t．

在Rt△PQB中，由勾股定理可知：PQ2=PB2+QB2，即（6﹣t）2+（2t）2=（12﹣2t）2．

解得：t1=﹣18+12，t2=﹣18﹣12（舍去）．

综上所述可知当t=0或t=﹣18+12时，⊙Q与四边形DPQC的一边相切．

②（Ⅰ）当t=0时，如图1所示：⊙Q与四边形DPQC有两个公共点；

（Ⅱ）如图3所示：当圆Q经过点D时，⊙Q与四边形DPQC有两个公共点．

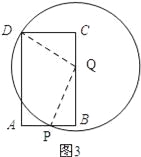
由题意可知：PB=6﹣t，BQ=2t，CQ=12﹣2t，DC=6．

由勾股定理可知：DQ2=DC2+CQ2=62+（12﹣2t）2，PQ2=PB2+QB2=（6﹣t）2+（2t）2．

∵DQ=PQ，

∴DQ2=PQ2，即62+（12﹣2t）2=（6﹣t）2+（2t）2．

整理得：t2+36t﹣144=0．

解得：t1=6﹣18，t2=﹣6﹣18（舍去）．

∴当0＜t＜6﹣18时，⊙Q与四边形DPQC有三个公共点．