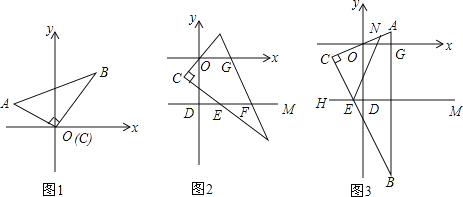
【题目】已知△ABC,∠ACB=90°,点D(0,-3),M(4,-3).
(1)如图1,若点C与点O重合,且A(-3,a),B(3,b),a+b-8=0,求△ACB的面积;
(2)如图2,若∠AOG=50°,求∠CEF的度数;
(3)如图3,旋转△ABC,使∠C的顶点C在直线DM与x轴之间,N为AC上一点,E为BC与DM的交点∠NEC+∠CEF=180°,下列两个结论:
①∠NEF-∠AOG为定值;②![]() 为定值,其中只有一个是正确的,请你判断出正确的结论,并求其值.
为定值,其中只有一个是正确的,请你判断出正确的结论,并求其值.
参考答案:
【答案】(1)△ACB的面积为12;(2)∠CEF的度数为140°;(3)![]() 为定值,其值为3.
为定值,其值为3.
【解析】试题分析:(1)过点A作AM⊥x轴于M,过点B作BN⊥x轴于N,根据![]() 的面积等于梯形
的面积等于梯形![]() 的面积减去两个直角三角形的面积列式计算即可得解;
的面积减去两个直角三角形的面积列式计算即可得解;
(2)根据对顶角相等和互余的性质得出![]() 再根据邻补角得出
再根据邻补角得出![]() 即可;
即可;
(3)作![]() 轴,则
轴,则![]() 轴,根据平行线的性质得
轴,根据平行线的性质得![]() 由于
由于![]() 所以
所以![]() 然后利用
然后利用![]() 即可得到
即可得到![]()
试题解析:(1)如图1,过点A作AM⊥x轴于M,过点B作BN⊥x轴于N,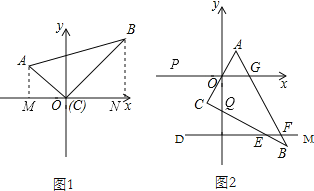
∵A(3,a),B(3,b),
∴AM=a,OM=3,BN=b,ON=3,
∴MN=3+3=6,
△ABC的面积![]()
∵a+b8=0,
∴a+b=8
∴△ABC的面积![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 为定值.理由如下:
为定值.理由如下:
作![]() 轴,如图3,
轴,如图3,
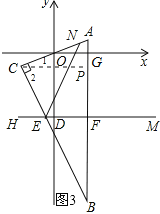
则![]() 轴,
轴,
![]()
而![]()
![]()
![]()
![]()
![]()
![]()
∴可得: ![]()
可得![]() 是定值.
是定值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,原点为O,点A(0,3),B(2,3),C(2,-3),D(0,-3).点P,Q是长方形ABCD边上的两个动点,BC交x轴于点M.点P从点O出发以每秒1个单位长度沿O→A→B→M的路线做匀速运动,同时点Q也从点O出发以每秒2个单位长度沿O→D→C→M的路线做匀速运动.当点Q运动到点M时,两动点均停止运动.设运动的时间为t秒,四边形OPMQ的面积为S.
(1)当t=2时,求S的值;
(2)若S<5时,求t的取值范围.
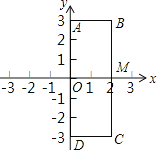
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算中,结果正确的是( )
A.(a﹣b)2=a2﹣b2
B.(﹣2)3=8
C.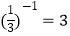
D.6a2÷2a2=3a2 -
科目: 来源: 题型:
查看答案和解析>>【题目】A、B两地相距450千米,甲、乙两车分别从A、B两地同时出发,相向而行.已知甲车速度为120千米/时,乙车速度为80千米/时,甲车出发半小时后发现有贵重物品未带于是立刻原速返回A地去取,再前往B地,问经过多长时间两车相距30km?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列是一名同学做的6道练习题:①(﹣3)0=1;②a3+a3=a6;③(﹣a5)÷(﹣a3)=﹣a2;④4m﹣2=
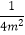 ;⑤(xy2)3=x3y6;⑥22+23=25 , 其中做对的题有( )
;⑤(xy2)3=x3y6;⑥22+23=25 , 其中做对的题有( )
A.1道
B.2道
C.3道
D.4道 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,O为坐标原点.三角形ABC的边BC在石轴上,点B的坐标是(-5,0),点A在y轴的正半轴上,点C在x轴的正半轴上,它们的坐标分别为A(0,m)、C(m-1,0),且OA+OC=7,动点P从点B出发,以每秒2个单位的速度,沿射线BO运动.设点P运动时间为t秒.
(1)求A、C两点的坐标;
(2)连结PA,当P沿射线BO匀速运动时,是否存在某一时刻,使三角形POA的面积是三角形ABC面积的
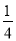 ?若存在,请求出t的值,并写出P点坐标;若不存在,请说明理由.
?若存在,请求出t的值,并写出P点坐标;若不存在,请说明理由.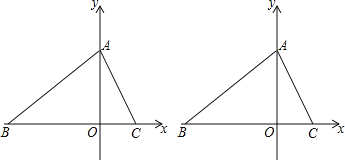
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市的商品房原价为12000元/m2,经过连续两次降价后,现价为9200元/m2,设平均每次降价的百分率为x,则根据题意可列方程为( )
A. 12000(1﹣2x)=9200B. 12000(1﹣x)2=9200
C. 9200(1+2x)=12000D. 9200(1+x)2=12000
相关试题

