【题目】综合与探究
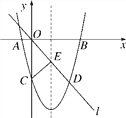
如图,在平面直角坐标系中,已知抛物线y=ax2+bx-8与x轴交于A,B两点,与y轴交于点C,直线l经过坐标原点O,与抛物线的一个交点为D,与抛物线的对称轴交于点E,连接CE,已知点A,D的坐标分别为(-2,0),(6,-8).
(1)求抛物线的解析式,并分别求出点B和点E的坐标;
(2)试探究抛物线上是否存在点F,使△FOE≌△FCE.若存在,请直接写出点F的坐标;若不存在,请说明理由.
参考答案:
【答案】(1) y=![]() x2-3x-8;(2)点F的坐标为(3+
x2-3x-8;(2)点F的坐标为(3+![]() ,-4)或(3-
,-4)或(3-![]() ,-4).
,-4).
【解析】试题分析:(1)把A、D坐标代入抛物线可求得抛物线的函数表达式,则抛物线的对称性可求得B点坐标,由D点坐标可求得直线OD的解析式,则可求得E点坐标;
(2)结合(1)可知OE=CE,由全等三角形的性质可知OF=CF,可知点F在线段OC的垂直平分线上,则可求得F点的纵坐标,代入抛物线解析式可求得F点的坐标.
试题解析:
(1)∵抛物线y=ax2+bx-8经过点A(-2,0),D(6,-8),
∴![]()
解得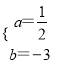
∴抛物线的函数表达式为y=![]() x23x8;
x23x8;
∵y=![]() x23x8=
x23x8=![]() (x3)2
(x3)2![]() ,
,
∴抛物线的对称轴为直线x=3.
又抛物线与x轴交于A,B两点,点A的坐标为(-2,0).
∴点B的坐标为(8,0),
设直线L的函数表达式为y=kx.
∵点D(6,-8)在直线L上,
∴6k=-8,解得k=-![]() ,
,
∴直线L的函数表达式为y=-![]() x,
x,
∵点E为直线L和抛物线对称轴的交点,
∴点E的横坐标为3,纵坐标为-![]() ×3=-4,
×3=-4,
∴点E的坐标为(3,-4);
(2)抛物线上存在点F,使△FOE≌△FCE.
∵OE=CE=5,
∴FO=FC,
∴点F在OC的垂直平分线上,此时点F的纵坐标为-4,
∴![]() x2-3x-8=-4,解得x=3±
x2-3x-8=-4,解得x=3±![]() ,
,
∴点F的坐标为(3-![]() ,-4)或(3+
,-4)或(3+![]() ,-4).
,-4).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在一条笔直的东西向海岸线l上有一长为1.5km的码头MN和灯塔C,灯塔C距码头的东端N有20km.一轮船以36km/h的速度航行,上午10:00在A处测得灯塔C位于轮船的北偏西30°方向,上午10:40在B处测得灯塔C位于轮船的北偏东60°方向,且与灯塔C相距12km.
(1)若轮船照此速度与航向航向,何时到达海岸线?
(2)若轮船不改变航向,该轮船能否停靠在码头?请说明理由(参考数据:
 ≈1.4,
≈1.4,  ≈1.7).
≈1.7).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边由长为30米的篱笆围成.已知墙长为18米(如图所示),设这个苗圃园垂直于墙的一边长为x米.
(1)若苗圃园的面积为72平方米,求x;
(2)若平行于墙的一边长不小于8米,这个苗圃园的面积有最大值和最小值吗?如果有,求出最大值和最小值;如果没有,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】设二次函数y1,y2的图象的顶点分别为(a,b)、(c,d),当a=﹣c,b=2d,且开口方向相同时,则称y1是y2的“反倍顶二次函数”.
(1)请写出二次函数y=x2+x+1的一个“反倍顶二次函数”;
(2)已知关于x的二次函数y1=x2+nx和二次函数y2=nx2+x,函数y1+y2恰是y1﹣y2的“反倍顶二次函数”,求n.
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着手机的普及,微信
 一种聊天软件
一种聊天软件 的兴起,许多人抓住这种机会,做起了“微商”,很多农产品也改变了原来的销售模式,实行了网上销售,这不刚大学毕业的小明把自家的冬枣产品也放到了网上,他原计划每天卖100斤冬枣,但由于种种原因,实际每天的销售量与计划量相比有出入,下表是某周的销售情况
的兴起,许多人抓住这种机会,做起了“微商”,很多农产品也改变了原来的销售模式,实行了网上销售,这不刚大学毕业的小明把自家的冬枣产品也放到了网上,他原计划每天卖100斤冬枣,但由于种种原因,实际每天的销售量与计划量相比有出入,下表是某周的销售情况 超额记为正,不足记为负
超额记为正,不足记为负 单位:斤
单位:斤 ;
;星期
一
二
三
四
五
六
日
与计划量的差值







(1)根据记录的数据可知前三天共卖出 ______ 斤;
(2)根据记录的数据可知销售量最多的一天比销售量最少的一天多销售 ______ 斤;
(3)本周实际销售总量达到了计划数量没有?
(4)若冬季每斤按8元出售,每斤冬枣的运费平均3元,那么小明本周一共收入多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形ABCD中,AE平分∠BAD,交BC于点E,且AB=AE,延长AB与DE的延长线交于点F,连接AC、CF. 下列结论:①△ABC≌△EAD;②△ABE是等边三角形;③AD=AF;④S△BEF=S△ABE.其中正确的有( )
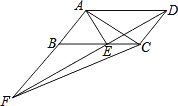
A.1个B.2个
C.3个D.4个
-
科目: 来源: 题型:
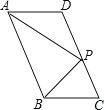
查看答案和解析>>【题目】如图,在平行四边形ABCD中,P是CD边上一点,且AP和BP分别平分∠DAB和∠CBA,若AD=5,AP=8,则△APB的面积是_______.
相关试题

