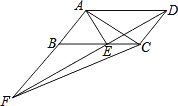
【题目】如图,平行四边形ABCD中,AE平分∠BAD,交BC于点E,且AB=AE,延长AB与DE的延长线交于点F,连接AC、CF. 下列结论:①△ABC≌△EAD;②△ABE是等边三角形;③AD=AF;④S△BEF=S△ABE.其中正确的有( )
A.1个B.2个
C.3个D.4个
参考答案:
【答案】B
【解析】
由四边形ABCD是平行四边形,可得![]() ,AD=BC,又因为AE平分
,AD=BC,又因为AE平分![]() ,可得
,可得![]() ,由AB=AE,得到△ABE是等边三角形,则
,由AB=AE,得到△ABE是等边三角形,则![]() ,所以△ABC≌△EAD,即可得到结果.
,所以△ABC≌△EAD,即可得到结果.
∵四边形ABCD是平行四边形,
∴![]() ,AD=BC,
,AD=BC,
∴![]() ,
,
又∵AE平分![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴AB=BE,
∵AB=AE,
∴△ABE是等边三角形,故②正确;
∴![]() ,
,
∵AB=AE,BC=AD,
∴△ABC≌△EAD,故①正确;
若AD与AF相等,即![]() ,
,
即EC=CD=BE,
即BC=2CD,
题中未限定这一条件,
∴③④不一定正确;
故正确的是①②正确;
故选:B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设二次函数y1,y2的图象的顶点分别为(a,b)、(c,d),当a=﹣c,b=2d,且开口方向相同时,则称y1是y2的“反倍顶二次函数”.
(1)请写出二次函数y=x2+x+1的一个“反倍顶二次函数”;
(2)已知关于x的二次函数y1=x2+nx和二次函数y2=nx2+x,函数y1+y2恰是y1﹣y2的“反倍顶二次函数”,求n.
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合与探究
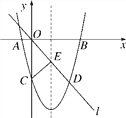
如图,在平面直角坐标系中,已知抛物线y=ax2+bx-8与x轴交于A,B两点,与y轴交于点C,直线l经过坐标原点O,与抛物线的一个交点为D,与抛物线的对称轴交于点E,连接CE,已知点A,D的坐标分别为(-2,0),(6,-8).
(1)求抛物线的解析式,并分别求出点B和点E的坐标;
(2)试探究抛物线上是否存在点F,使△FOE≌△FCE.若存在,请直接写出点F的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着手机的普及,微信
 一种聊天软件
一种聊天软件 的兴起,许多人抓住这种机会,做起了“微商”,很多农产品也改变了原来的销售模式,实行了网上销售,这不刚大学毕业的小明把自家的冬枣产品也放到了网上,他原计划每天卖100斤冬枣,但由于种种原因,实际每天的销售量与计划量相比有出入,下表是某周的销售情况
的兴起,许多人抓住这种机会,做起了“微商”,很多农产品也改变了原来的销售模式,实行了网上销售,这不刚大学毕业的小明把自家的冬枣产品也放到了网上,他原计划每天卖100斤冬枣,但由于种种原因,实际每天的销售量与计划量相比有出入,下表是某周的销售情况 超额记为正,不足记为负
超额记为正,不足记为负 单位:斤
单位:斤 ;
;星期
一
二
三
四
五
六
日
与计划量的差值







(1)根据记录的数据可知前三天共卖出 ______ 斤;
(2)根据记录的数据可知销售量最多的一天比销售量最少的一天多销售 ______ 斤;
(3)本周实际销售总量达到了计划数量没有?
(4)若冬季每斤按8元出售,每斤冬枣的运费平均3元,那么小明本周一共收入多少元?
-
科目: 来源: 题型:
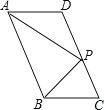
查看答案和解析>>【题目】如图,在平行四边形ABCD中,P是CD边上一点,且AP和BP分别平分∠DAB和∠CBA,若AD=5,AP=8,则△APB的面积是_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】结合数轴与绝对值的知识回答下列问题:
(1)表示﹣3和2两点之间的距离是_____;一般地,数轴上表示数m和数n的两点之间的距离等于|m﹣n|.
如果|a+2|=3,那么a=_____;
(2)若数轴上表示数a的点位于﹣4与2之间,则|a+4|+|a﹣2|的值为_____;
(3)利用数轴找出所有符合条件的整数点x,使得|x+2|+|x﹣5|=7,这些点表示的数的和是_____;
(4)当a=_____时,|a+3|+|a﹣1|+|a﹣4|的值最小,最小值是_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】求若干个相同的不为零的有理数的除法运算叫做除方. 如:2÷2÷2,(-3)÷(-3)÷(-3 )÷( -3)等. 类比有理数的乘方,我们把 2÷2÷2 记作 2③,读作“2 的圈 3 次方”. (-3)÷(-3)÷(-3 )÷( -3)记作(-3)④,读作“-3 的圈 4 次方”.
一般地,把
 (a≠0)记作a,记作“a 的圈c次方”.
(a≠0)记作a,记作“a 的圈c次方”.(1)直接写出计算结果:2③= ,(-3)④ = ,
 ⑤= .
⑤= .(2)计算 24÷23 + (-8)×2③.
相关试题

