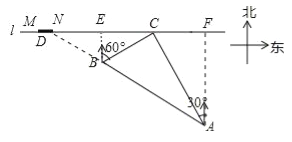
【题目】如图,在一条笔直的东西向海岸线l上有一长为1.5km的码头MN和灯塔C,灯塔C距码头的东端N有20km.一轮船以36km/h的速度航行,上午10:00在A处测得灯塔C位于轮船的北偏西30°方向,上午10:40在B处测得灯塔C位于轮船的北偏东60°方向,且与灯塔C相距12km.
(1)若轮船照此速度与航向航向,何时到达海岸线?
(2)若轮船不改变航向,该轮船能否停靠在码头?请说明理由(参考数据: ![]() ≈1.4,
≈1.4, ![]() ≈1.7).
≈1.7).

参考答案:
【答案】(1)11:00;(2)能,理由见解析.
【解析】试题分析:(1)延长AB交海岸线l于点D,过点B作BE⊥海岸线l于点E,过点A作AF⊥l于F,易证△ABC是直角三角形,再证明∠BAC=30°,再求出BD的长即可解决问题.(2)在RT△BEC中,求出CD的长度,和CN、CM比较即可解决问题.
试题解析:(1)延长AB交海岸线l于点D,过点B作BE⊥海岸线l于点E,过点A作AF⊥l于F,如图所示.
∵∠BEC=∠AFC=90°,∠EBC=60°,∠CAF=30°,
∴∠ECB=30°,∠ACF=60°,
∴∠BCA=90°,
∵BC=12,AB=36×![]() =24,
=24,
∴AB=2BC,
∴∠BAC=30°,∠ABC=60°,
∵∠ABC=∠BDC+∠BCD=60°,
∴∠BDC=∠BCD=30°,
∴BD=BC=12,
∴时间t=![]() =
=![]() 小时=20分钟,
小时=20分钟,
∴轮船照此速度与航向航向,上午11::00到达海岸线.
(2)∵BD=BC,BE⊥CD,
∴DE=EC,
在RT△BEC中,∵BC=12,∠BCE=30°,
∴BE=6,EC=6![]() ≈10.2,
≈10.2,
∴CD=20.4,
∵20<20.4<21.5,
∴轮船不改变航向,轮船可以停靠在码头.
-
科目: 来源: 题型:
查看答案和解析>>【题目】知三角形的两边长分别为4cm和9cm,则下列长度的四条线段中能作为第三边的是( )
A. 13cmB. 6cmC. 5cmD. 4cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:2x2+4x+2= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】求x的值:(x-3)2=25
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式中,正确的是( )
A. 30=0 B. x3x2=x5 C. (x﹣1)2=x2﹣1 D. x﹣2x=x
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个角的补角是128°37″那么这个角的余角是______________
-
科目: 来源: 题型:
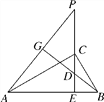
查看答案和解析>>【题目】如图,已知CE是Rt△ABC斜边AB上的高,在EC的延长线上任取一点P,连接AP,作BG⊥AP,垂足为G,交CE于D,求证:CE2=PE·DE.
相关试题

