搜索
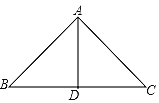
【题目】如图，∠BAC=90°，AD⊥BC，垂足为点 D.下列说法中：①∠B的余角只有∠BAD；②∠B=∠C；③线段 AB 的长度表示点 B 到直线 AC 的距离；④AB·AC=BC·AD；一定正确的有( )
A. 1 个 B. 2 个 C. 3 个 D. 4 个
参考答案：
【答案】A
【解析】
根据互为余角的定义，点的线的距离就是点到线的垂线段的长度及相似三角形的判定解答即可.
∠B的余角有∠BAD和∠C, ①错误; ∵∠BAC=90°, ∴∠B+∠C=90°, ②错误; 点 B 到直线 AC 的距离是线段BA的长度, ③错误; ∵∠B+∠C=90°, ∠C+∠CAD=90°, ∴∠B=∠CAD, ∵∠BAC=∠ADC=90°, ∴△ABC∽△DAC, ∴
, ∴AB·AC=BC·AD,④正确.故选A.
-
科目： 来源： 题型：
查看答案和解析>>【题目】等边三角形ABC的边长为6，在AC，BC边上各取一点E、F，连接AF，BE相交于点P，若AE=CF，则∠APB=______.
-
科目： 来源： 题型：
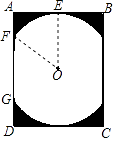
查看答案和解析>>【题目】某景区修建一栋复古建筑，其窗户设计如图所示．圆O的圆心与矩形ABCD对角线的交点重合，且圆与矩形上下两边相切（E为上切点），与左右两边相交（F，G为其中两个交点），图中阴影部分为不透光区域，其余部分为透光区域．已知圆的半径为1m，根据设计要求，若∠EOF=45°，则此窗户的透光率（透光区域与矩形窗面的面积的比值）为 ．
-
科目： 来源： 题型：
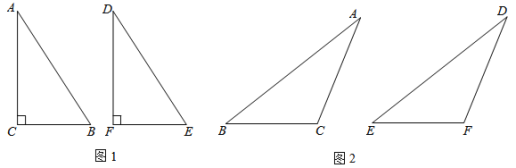
查看答案和解析>>【题目】学习全等三角形的判定方法以后，我们知道“已知两边和一角分别相等的两个三角形不一定全等”，但下列两种情形还是成立的．
（1）第一情形（如图1）在△ABC和△DEF中，∠C=∠F=90°，AC=DF，AB=DE，则根据__________，得出△ABC≌△DEF；
（2）第二情形（如图2）在△ABC和△DEF中，∠C=∠F（∠C和∠F均为钝角），AC=DF，AB=DE，求证：△ABC≌△DEF.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知△ABC中，AB=AC=10厘米，BC=8厘米，点D为AB 的中点．如果点P在线段BC上以3厘米/秒的速度由B点向C点运动，同时点Q在线段CA上由C点向A点运动．当一个点停止运动时时，另一个点也随之停止运动．设运动时间为t．
（1）用含有t的代数式表示CP．
（2）若点Q的运动速度与点P的运动速度相等，经过1秒后，△BPD与△CQP是否全等，请说明理由；
（3）若点Q的运动速度与点P的运动速度不相等，当点Q的运动速度为多少时，能够使△BPD与△CQP全等？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，矩形ABCD中，O为AC的中点，过点O的直线分别与AB，CD交于点E，F，连接BF交AC于点M，连接DE，BO.若∠COB＝60°，FO＝FC，则下列结论：①FB⊥OC，OM＝CM；②△EOB≌△CMB；③四边形EBFD是菱形；④MB∶OE＝3∶2.其中正确结论的个数是（ ）
A. 1 B. 2 C. 3 D. 4
-
科目： 来源： 题型：
查看答案和解析>>【题目】(1)已知一个角的补角比它的余角的 3 倍大 30°，求这个角的度数；
(2)如图，点 C、D在线段 AB上， D是线段 AB的中点， AC
AD ， AB6，求线段 CD的长．
相关试题
