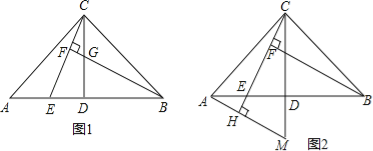
【题目】如图,在△ABC中,AC=BC,∠ACB=90°,D是AB的中点,点E是AB边上一点.
(1)BF⊥CE于点F,交CD于点G(如图①).求证:AE=CG;
(2)AH⊥CE,垂足为H,交CD的延长线于点M(如图②),找出图中与BE相等的线段,并证明.

参考答案:
【答案】(1)证明见解析(2)BE=CM.证明见解析.
【解析】试题分析:(1)首先根据点D是AB中点,∠ACB=90°,可得出∠ACD=∠BCD=45°,判断出△AEC≌△CGB,即可得出AE=CG,
(2)根据垂直的定义得出∠CMA+∠MCH=90°,∠BEC+∠MCH=90°,再根据AC=BC,∠ACM=∠CBE=45°,得出△BCE≌△CAM,进而证明出BE=CM.
(1)证明:∵点D是AB中点,AC=BC,
∠ACB=90°,
∴CD⊥AB,∠ACD=∠BCD=45°,
∴∠CAD=∠CBD=45°,
∴∠CAE=∠BCG,
又∵BF⊥CE,
∴∠CBG+∠BCF=90°,
又∵∠ACE+∠BCF=90°,
∴∠ACE=∠CBG,
在△AEC和△CGB中,
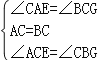
∴△AEC≌△CGB(ASA),
∴AE=CG,
(2)解:BE=CM.
证明:∵CH⊥HM,CD⊥ED,
∴∠CMA+∠MCH=90°,∠BEC+∠MCH=90°,
∴∠CMA=∠BEC,
又∵∠ACM=∠CBE=45°,
在△BCE和△CAM中,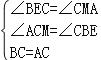 ,
,
∴△BCE≌△CAM(AAS),
∴BE=CM.
-
科目: 来源: 题型:
查看答案和解析>>【题目】瑞安市新行政区划调整为5镇10街道,市区总人口687498人,将这个总人口数保留两个有效数字并用科学记数法表示,则为( ).
A.6.8×105 B.6.9×105 C.68×104 D.69×104
-
科目: 来源: 题型:
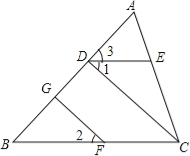
查看答案和解析>>【题目】∠1=∠2,∠3=∠B,FG⊥AB于G,猜想CD与AB的关系,并证明你的猜想.
-
科目: 来源: 题型:
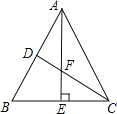
查看答案和解析>>【题目】如图,在△ABC中,∠BAC=50°,∠B=60°,AE⊥BC于点E,CD平分∠ACB且分别与AB、AE交于点D、F,求∠AFC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有50个数据,共分成6组,第1~4组的频数分别为10,8,7,11.第5组的频率是0.16,则第6组的频数是__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a-7b=-2,则4-2a+14b的值是( ).
A. 0 B. 2 C. 4 D. 8
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列图形中,对称轴有且只有3条的是( )
A. 菱形 B. 等边三角形 C. 正方形 D. 圆
相关试题

