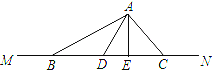
【题目】如图,MN是一条东西朝向的笔直的公路,C是位于该公路上的一个检测点辆长为9m的小货车BD行驶在该公路上小王位于点A处观察小货车,某时刻他发现车头D、车尾B及检测点C分别距离他10m、17m,2![]() m
m
(1)过点A向MN引垂线,垂足为E,请利用勾股定理分别找出线段AE与DE、AE与BE之间所满足的数量关系;
(2)在上一问的提示下,继续完成下列问题:
①求线段DE的长度;
②该小货车的车头D距离检测点C还有多少m?
参考答案:
【答案】(1)289(2)①6(2)16
【解析】
(1)有勾股定理即可得出AE与DE、AE与BE之间所满足的数量关系;
(2)由(1)中两式相减得:BE2﹣DE2=189推出BD=BE﹣DE=9,BE+DE=BD+DE+DE=9+2DE,
再推出BE2﹣DE2=(BE+DE)(BE﹣DE)=9(9+2DE)=189,求出DE;
再利用勾股定理求出AE,即可求出该小货车的车头D距离检测点C还有多少m.
(1)在直角△ADE中,∵∠AED=90°,AD=10,
∴AE2+DE2=AD2=100,
在直角△ABE中,∵∠AEB=90°,AB=17,
∴AE2+BE2=AB2=289;
(2)①两式相减,得:BE2﹣DE2=189,
∴BD=BE﹣DE=9,BE+DE=BD+DE+DE=9+2DE,
∴BE2﹣DE2=(BE+DE)(BE﹣DE)=9(9+2DE)=189,
∴DE=6;
②在直角△ADE中,∵∠AED=90°,
∴AE= ![]() =8,
=8,
在Rt△AEC中,CE= ![]() =10,
=10,
∴CD=CE+DE=16.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,将抛物线C1:y=x2+3先向右平移1个单位,再向下平移7个单位得到抛物线C2 . C2的图象与x轴交于A、B两点(点A在点B的左侧).
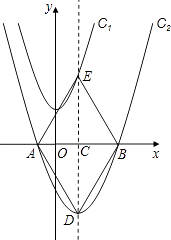
(1)求抛物线C2的解析式;
(2)若抛物线C2的对称轴与x轴交于点C,与抛物线C2交于点D,与抛物线C1交于点E,连结AD、DB、BE、EA,请证明四边形ADBE是菱形,并计算它的面积;
(3)若点F为对称轴DE上任意一点,在抛物线C2上是否存在这样的点G,使以O、B、F、G四点为顶点的四边形是平行四边形?如果存在,请求出点G的坐标;如果不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)8+(﹣
 )﹣5﹣(﹣0.25)
)﹣5﹣(﹣0.25)(2)﹣82+72÷36
(3)﹣4.2+5.7﹣8.4﹣2.3
(4)25×
 +25×(﹣
+25×(﹣ )
)(5)|﹣0.2|﹣|﹣3﹣(+8)|﹣|﹣8﹣2+10|
(6)(﹣5)×(﹣8)×(﹣2.5)×9
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A(a,6)是第一象限内正比例函数y=3x的图象上的一点,AB⊥x轴,交直线OB于B点,三角形OAB的面积为5,求直线OB所对应的函数表达式.

-
科目: 来源: 题型:
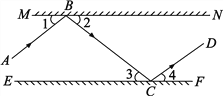
查看答案和解析>>【题目】如图所示,MN、EF分别表示两个互相平行的镜面,一束光线AB照射到镜面MN上,反射光线为BC,此时∠1=∠2;光线BC经过镜面EF反射后的光线为CD,此时∠3=∠4.试判断AB与CD的位置关系,你是如何思考的?
-
科目: 来源: 题型:
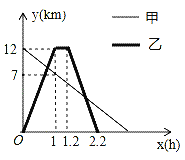
查看答案和解析>>【题目】某地植物园从正门到侧门有一条小路,甲徒步从正门出发匀速走向侧门,乙与甲同时出发,骑自行车从侧门匀速前往正门到达正门后休息0.2小时,然后按原路原速匀速返回侧门,图中折线分别表示甲、乙到侧门的距离y(km)与出发时间x(h)之间的函数关系图象,根据图象信息解答下列问题:
(1)求甲到侧门的距离y与x之间的函数关系式;
(2)求甲、乙第一次相遇时到侧门的距离.
(3)求甲、乙第二次相遇的时间.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A(a,6)是第一象限内正比例函数y=3x的图象上的一点,AB⊥x轴,交直线OB于B点,三角形OAB的面积为5,求直线OB所对应的函数表达式.

相关试题

