【题目】将九年级部分男生掷实心球的成绩进行整理,分成5个小组(x表示成绩,单位:米).A组:5.25≤x<6.25;B组:6.25≤x<7.25;C组:7.25≤x<8.25;D组:8.25≤x<9.25;E组:9.25≤x<10.25,并绘制出扇形统计图和频数分布直方图(不完整).规定x≥6.25为合格,x≥9.25为优秀.
(1)这部分男生有多少人?其中成绩合格的有多少人?
(2)这部分男生成绩的中位数落在哪一组?扇形统计图中D组对应的圆心角是多少度?
(3)要从成绩优秀的学生中,随机选出2人介绍经验,已知甲、乙两位同学的成绩均为优秀,求他俩至少有1人被选中的概率.
参考答案:
【答案】
(1)
解:∵A组占10%,有5人,
∴这部分男生共有:5÷10%=50(人);
∵只有A组5人成绩不合格,
∴合格人数为:50﹣5=45(人);
(2)
解:∵C组占30%,共有人数:50×30%=15(人),B组有10人,D组有15人,
∴这50人男生的成绩由低到高分组排序,A组有5人,B组有10人,C组有15人,D组有15人,E组有5人,
∴成绩的中位数落在C组;
∵D组有15人,占15÷50=30%,
∴对应的圆心角为:360°×30%=108°;
(3)
解:成绩优秀的男生在E组,含甲、乙两名男生,记其他三名男生为a,b,c,
画树状图得:
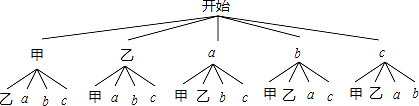
∵共有20种等可能的结果,他俩至少有1人被选中的有14种情况,
∴他俩至少有1人被选中的概率为: ![]() =
= ![]() .
.
【解析】(1)根据“部分÷百分比=总数”解得总人数;再根据题意得不合格的分数,从而知A组为不合格的分数;
(2)一组数据从小到大的顺序排列,排在最中间的数是中位数;圆心角度数=360°×百分比;
(3)用列表法或树状图,列出所有等可能的结果,再找出事件出现的结果数,从而用概率公式计算概率 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,菱形OBCD的边OB在x轴上,反比例函数y=
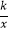 (x>0)的图象经过菱形对角线的交点A,且与边BC交于点F,点A的坐标为(4,2).则点F的坐标是
(x>0)的图象经过菱形对角线的交点A,且与边BC交于点F,点A的坐标为(4,2).则点F的坐标是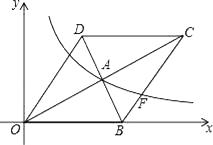
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合题
(1)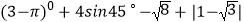
.
(2)解分式方程: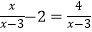
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小俊在A处利用高为1.5米的测角仪AB测得楼EF顶部E的仰角为30°,然后前进12米到达C处,又测得楼顶E的仰角为60°,求楼EF的高度.(结果保留根号)
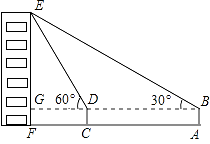
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=AC,D是线段BC的延长线上一点,以AD为一边在AD的右侧作△ADE,使AE=AD,∠DAE=∠BAC,连接CE.
(1)如图1,点D在线段BC的延长线上移动,若∠BAC=30°,则∠DCE= .
(2)设∠BAC=α,∠DCE=β:
①如图1,当点D在线段BC的延长线上移动时,α与β之间有什么数量关系?请说明理由;
②当点D在直线BC上(不与B、C重合)移动时,α与β之间有什么数量关系?请直接写出你的结论.

-
科目: 来源: 题型:
查看答案和解析>>【题目】为加强中小学生安全和禁毒教育,某校组织了“防溺水、交通安全、禁毒”知识竞赛,为奖励在竞赛中表现优异的班级,学校准备从体育用品商场一次性购买若干个足球和篮球(每个足球的价格相同,每个篮球的价格相同),购买1个足球和1个篮球共需159元;足球单价是篮球单价的2倍少9元.
(1)求足球和篮球的单价各是多少元?
(2)根据学校实际情况,需一次性购买足球和篮球共20个,但要求购买足球和篮球的总费用不超过1550元,学校最多可以购买多少个足球? -
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列各式:13=1=
 ;13+23=9=
;13+23=9=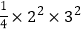 ;13+23+33=36=
;13+23+33=36= ;13+23+33+43=100=
;13+23+33+43=100= ,
,回答下面的问题:
(1)13+23+33+43+…+103=_____(写出算式即可);
(2)计算13+23+33+…+993+1003的值;
(3)计算:113+123+…+993+1003的值.
相关试题

