Question

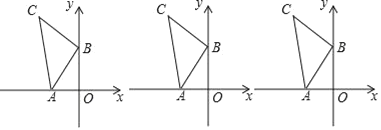
【题目】如图，A(m，0)，B(0，n)，以B点为直角顶点在第二象限作等腰直角△ABC.

(1)求C点的坐标.

(2)在y轴右侧的平面内是否存在一点P，使△PAB与△ABC全等？若存在，求出P点坐标，若不存在，请说明理由.

Answer 1

【答案】(1)点C的坐标为(﹣n，n﹣m)；(2)存在，P点坐标为(n，n+m)或(m+n，m).

【解析】

(1)过点C作CD⊥y轴于点D，由△ABC为等腰直角三角形即可得出∠ABC=90°、AB=BC，通过角的计算即可得出∠ABO=∠BCD，再结合∠CDB=∠BOA=90°即可利用AAS证出△ABO和△BCD，由此即可得出BD、CD的长度，进而可得出点C的坐标；

(2)△PAB与△ABC全等分两种情况：①当∠ABP=90°时，根据∠ABC=∠ABP=90°、△ABC≌△ABP，即可得出点C、P关于点B对称，结合点B、C的坐标即可得出点P的坐标；②当∠BAP=90°时，由∠ABC=∠BAP=90°即可得出BC∥AP，根据△ABC≌△BAP即可得出BC=AP，进而可找出四边形APBC为平行四边形，结合点A、B、C的坐标即可找出点P的坐标.综上即可得出结论.

解：(1)过点C作CD⊥y轴于点D，如图1所示.

∵△ABC为等腰直角三角形，

∴∠ABC=90°，AB=BC.

∵CD⊥BD，BO⊥AO，

∴∠CDB=∠BOA=90°.

∵∠CBD+∠ABO=90°，∠CBD+∠BCD=90°，

∴∠ABO=∠BCD.

∴△ABO≌△BCD(AAS)，

∴BD=AO，CD=BO，

∵A(m，0)，B(0，n)，

∴BD=﹣m，CD=n，

∴点C的坐标为(﹣n，n﹣m).

(2)△PAB与△ABC全等分两种情况：

①当∠ABP=90°时，如图2所示.

∵∠ABC=∠ABP=90°，△ABC≌△ABP，

∴点C、P关于点B对称，

∵C(﹣n，n﹣m)，B(0，n)，

∴点P的坐标为(n，n+m)；

②当∠BAP=90°时，如图3所示.

∵△ABC≌△BAP，

∴∠ABC=∠BAP=90°，BC=AP，

∴BC∥AP，

∴四边形APBC为平行四边形.

∵A(m，0)、B(0，n)，C(﹣n，n﹣m)，

∴点P的坐标为(m+n，m).

综上所述：在y轴右侧的平面内存在一点P，使△PAB与△ABC全等，P点坐标为(n，n+m)或(m+n，m).