【题目】在△ABC中,AB=AC,点D在边BC所在的直线上,过点D作DE∥AC交直线AB于点E,DF∥AB交直线AC于点F.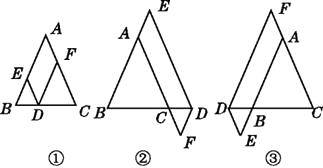
(1)当点D在边BC上时,如图①,求证:DE+DF=AC.
(2)当点D在边BC的延长线上时,如图②;当点D在边BC的反向延长线上时,如图③.请分别写出图②、图③中DE,DF,AC之间的数量关系,不需要证明.
(3)若AC=6,DE=4,则DF=.
参考答案:
【答案】
(1)证明:∵DE∥AC,DF∥AB,
∴∠FDC=∠B,四边形AEDF是平行四边形.
∴DE=AF.
又∵AB=AC,∴∠B=∠C,
∴∠FDC=∠C,∴DF=FC,
∴DE+DF=AF+FC=AC
(2)解:当点D在边BC的延长线上时,DE-DF=AC;
∵DE∥AC,DF∥AB,
∴∠FDC=∠B,四边形AEDF是平行四边形.
∴DE=AF.
又∵AB=AC,∴∠B=∠ACB,
∴∠FDC=∠ACB,
∵∠DCF=∠ACB,
∴∠FDC=∠DCF
∴DF=FC,
∴AC+CF=AC+DF=AF=DE
DE-DF=AC;
同理可证当点D在边BC的反向延长线上时,DF-DE=AC
(3)2或10
【解析】(3)根据(1)的结论DE+DF=AC
∵AC=6,DE=4
∴DF=AC-DE=6-4=2
根据图②的结论DE-DF=AC
∴DF=DE-AC=-2,不符合题意;
根据图③的结论DF-DE=AC
∴DF=DE+AC=4+6=10
(1)根据已知条件及平行四边形的判定,可证明四边形AEDF是平行四边形,得出DE=AF,再根据等腰三角形的性质及平行线的性质证明∠FDC=∠C,得到DF=FC,然后根据DE+DF=AF+FC,即可证得结论。
(2)图②根据已知条件及平行四边形的判定,可证明四边形AEDF是平行四边形,得出DE=AF,再根据等腰三角形的性质及平行线的性质证明∠FDC=∠DCF,得到DF=FC,然后根据AC+CF=AC+DF=AF=DE,即可证得结论;同理可得出图③的结论。
(3)利用(1)(2)(3)的结论计算即可。
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列两项中,属于同类项的是( )
A.62与x2B.4ab与4abcC.0.2x2y与0.2xy2D.nm和﹣mn
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,AC=5cm,∠BAC=60°,动点M从点B出发,在BA边上以每秒2cm的速度向点A匀速运动,同时动点N从点C出发,在CB边上以每秒
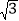 cm的速度向点B匀速运动,设运动时间为t秒(0≤t≤5),连接MN.
cm的速度向点B匀速运动,设运动时间为t秒(0≤t≤5),连接MN.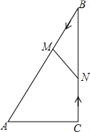
(1)若BM=BN,求t的值;
(2)若△MBN与△ABC相似,求t的值;
(3)当t为何值时,四边形ACNM的面积最小?并求出最小值.
-
科目: 来源: 题型:
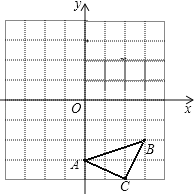
查看答案和解析>>【题目】已知:如图△ABC三个顶点的坐标分别为A(0,﹣3)、B(3,﹣2)、C(2,﹣4),正方形网格中,每个小正方形的边长是1个单位长度.
(1)画出△ABC向上平移6个单位得到的△A1B1C1;
(2)以点C为位似中心,在网格中画出△A2B2C2,使△A2B2C2与△ABC位似,且△A2B2C2与△ABC的位似比为2:1,并直接写出点A2的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果2是方程x2﹣3x+k=0的一个根,则常数k的值为( )
A.1
B.2
C.﹣1
D.﹣2 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.(2a2)3=6a6
B.-a2b2·3ab3=-3a2b5
C.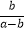 +
+ 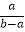 =-1
=-1
D.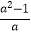 ·
· 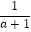 =-1
=-1 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式中,正确的是( )
A.m5m5=2m10
B.m4m4=m8
C.m3m3=m9
D.m6+m6=2m12
相关试题

