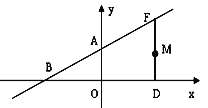
【题目】如图,一次函数![]() 的图象交y轴于点A,交x轴于点B,点F在射线BA上,过点F作x轴的垂线,点D为垂足,
的图象交y轴于点A,交x轴于点B,点F在射线BA上,过点F作x轴的垂线,点D为垂足,
⑴若OD=6,求F点的坐标;
(2)若OD=12,M在线段FD上,M的纵坐标为m,连接BM,用含有m的代数式表示△BMF的面积.
参考答案:
【答案】(1)![]() ;(2)150-10m
;(2)150-10m
【解析】
(1)分点D在x轴正半轴和负半轴两种情况讨论即可;
(2)先求得B的坐标,即可得到BD的长,再令x=12,求得点F的坐标,即可得到FM的长,再利用三角形面积公式即可表示出△BMF的面积.
(1)∵OD=6,
∴点D横坐标为6或-6,
∴当x=6时,把x=6代入到![]() 中,得y=
中,得y=![]() ,得
,得![]() ;
;
当x=-6时,把x=-6代入到![]() 中,得y=
中,得y=![]() ,得
,得![]() ;
;
故点![]() ;
;
(2)令y=0,得![]() =0,解得x=-8,
=0,解得x=-8,
∴B(-8,0),
把x=12代入到![]() 中,得y=
中,得y=![]() ,得
,得![]() ,
,
∴FM=15-m,BD=8+12=20,
∴S△BMF=![]() FM·BD=
FM·BD=![]() ×(15-m) ×20=150-10m;
×(15-m) ×20=150-10m;
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,长方形OABC中,O为平面直角坐标系的原点,A点的坐标为(4,0),C点的坐标为(0,6),点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O﹣C﹣B﹣A﹣O的路线移动(即:沿着长方形移动一周).
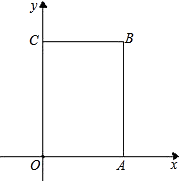
(1)写出B点的坐标();
(2)当点P移动了4秒时,描出此时P点的位置,并写出点P的坐标.
(3)在移动过程中,当点P到x轴距离为5个单位长度时,求点P移动的时间. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知平面内有两条直线AB、CD,且AB∥CD,P为一动点.
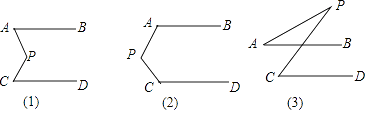
(1)当点P移动到AB、CD之间时,如图(1),这时∠P与∠A、∠C有怎样的关系?证明你的结论;
(2)当点P移动到图(2)、图(3)的位置时,∠P、∠A、∠C又有怎样的关系?请分别写出你的结论. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列几何体中,主视图、俯视图、左视图都相同的是( )
A.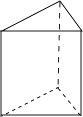
B.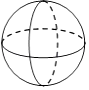
C.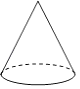
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,AC=BC=1,将Rt△ABC绕点A逆时针旋转30°后得到Rt△ADE,点B经过的路径为
 ,则图中阴影部分的面积是( )
,则图中阴影部分的面积是( ) 
A.
B.
C. ﹣
﹣ 
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中描出点 A(﹣2,0)、B(3,1)、C(2,3),将各点用线段依次 连接起来,并解答如下问题:
(1)在平面直角坐标系中画出△ A′B′C′,使它与△ ABC 关于 x 轴对称,并直接写出△ A′B′C′三个顶点的坐标;
(2)求△ABC的面积.
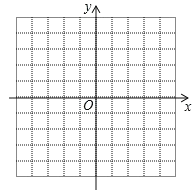
-
科目: 来源: 题型:
查看答案和解析>>【题目】小李从西安通过某快递公司给在南昌的外婆寄一盒樱桃,快递时,他了解到这个公司除收取每次6元的包装费外,樱桃不超过1kg收费22元,超过1kg,则超出部分按每千克10元加收费用.设该公司从西安到南昌快递樱桃的费用为y(元),所寄樱桃为x(kg).
(1)求y与x之间的函数关系式;
(2)已知小李给外婆快寄了2.5kg樱桃,请你求出这次快寄的费用是多少元?
相关试题

