【题目】我们知道,任意一个正整数n都可以进行这样的分解:n=p×q(p,q是正整数,且p≤q),在n的所有这种分解中,如果p,q两因数之差的绝对值最小,我们就称p×q是n的最佳分解.并规定:F(n)=![]() .例如12可以分解成1×12,2×6或3×4,因为12﹣1>6﹣2>4﹣3,所有3×4是12的最佳分解,所以F(12)=
.例如12可以分解成1×12,2×6或3×4,因为12﹣1>6﹣2>4﹣3,所有3×4是12的最佳分解,所以F(12)=![]() .
.
(1)如果一个正整数a是另外一个正整数b的平方,我们称正整数a是完全平方数.求证:对任意一个完全平方数m,总有F(m)=1;
(2)如果一个两位正整数t,t=10x+y(1≤x≤y≤9,x,y为自然数),交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差为18,那么我们称这个数t为“吉祥数”,求所有“吉祥数”中F(t)的最大值.
参考答案:
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题分析:(1)根据题意可设m=![]() ,由最佳分解定义可得F(m)=
,由最佳分解定义可得F(m)=![]() =1;
=1;
(2)根据“吉祥数”定义知(10y+x)﹣(10x+y)=18,即y=x+2,结合x的范围可得2位数的“吉祥数”,求出每个“吉祥数”的F(t),比较后可得最大值.
试题解析:(1)对任意一个完全平方数m,设m=![]() (n为正整数),∵|n﹣n|=0,∴n×n是m的最佳分解,∴对任意一个完全平方数m,总有F(m)=
(n为正整数),∵|n﹣n|=0,∴n×n是m的最佳分解,∴对任意一个完全平方数m,总有F(m)=![]() =1;
=1;
(2)设交换t的个位上的数与十位上的数得到的新数为t′,则t′=10y+x,∵t为“吉祥数”,∴t′﹣t=(10y+x)﹣(10x+y)=9(y﹣x)=18,∴y=x+2,∵1≤x≤y≤9,x,y为自然数,∴“吉祥数”有:13,24,35,46,57,68,79,∴F(13)=![]() ,F(24)=
,F(24)=![]() =
=![]() ,F(35)=
,F(35)=![]() ,F(46)=
,F(46)=![]() ,F(57)=
,F(57)=![]() ,F(68)=
,F(68)=![]() ,F(79)=
,F(79)=![]() ,∵
,∵![]() >
>![]() >
>![]() >
>![]() >
>![]() >
>![]() >
>![]() ,∴所有“吉祥数”中,F(t)的最大值是
,∴所有“吉祥数”中,F(t)的最大值是![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】以下列各组数为边的三角形中,是直角三角形的有( )
(1)3,4,5;(2)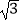 ,
, 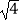 ,
, 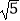 ;(3)32 , 42 , 52;(4)0.03,0.04,0.05.
;(3)32 , 42 , 52;(4)0.03,0.04,0.05.
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列图形中,既是中心对称图形又是轴对称图形的是( )
A.角
B.等边三角形
C.平行四边形
D.圆 -
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=x2﹣2x+3向上平移2个单位长度,再向右平移3个单位长度后,得到的抛物线的解析式为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列不等式中,是一元一次不等式的是( )
A.2x-1>0
B.-1<2
C.3x-2y≤-1
D.y2+3>5 -
科目: 来源: 题型:
查看答案和解析>>【题目】一袋中装有形状大小都相同的四个小球,每个小球上各标有一个数字,分别是1,4,7,8.现规定从袋中任取一个小球,对应的数字作为一个两位数的个位数;然后将小球放回袋中并搅拌均匀,再任取一个小球,对应的数字作为这个两位数的十位数.
(1)写出按上述规定得到所有可能的两位数;
(2)从这些两位数中任取一个,求其算术平方根大于4且小于7的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,图2中,∠1和∠2,∠3和∠4各是哪两条直线被哪一条直线所截形成的?它们各是什么位置关系的角?
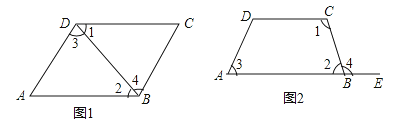
相关试题

