【题目】如图,△ABC中,点E是BC上的一点,BC=3BE,点D是AC的中点,若S△ADF﹣S△BEF=2.则S△ABC=_____.

参考答案:
【答案】12
【解析】
如图,取AE的中点H,连接DH.首先证明S△AHD=2,求出△AEC,△ABE的面积即可解决问题.
如图,取AE的中点H,连接DH.
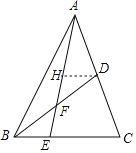
∵AH=HE,AD=DC,
∴DH∥BC,EC=2DH,
∵BC=3BE,
∴EC=2BE,
∴BE=DH,
∵∠HDF=∠EBF,∠HFD=∠EFB,BE=DH,
∴△HDF≌△EBF(AAS),
∴S△EBF=S△HDF,
∵S△ADF﹣S△BEF=2,
∴S△AHD=2,
∵DH∥EC,
∴△AHD∽△AEC,
∴![]() ,
,
∴S△AEC=8,
∵EC=2BE,
∴S△ABE=4,
∴S△ABC=12.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC,∠BAC=40°,将△ABC绕点A按逆时针方向旋转100°.得到△ADE,连接BD,CE交于点F.
(1)求证:△ABD≌△ACE;
(2)求证:四边形ABFE是菱形.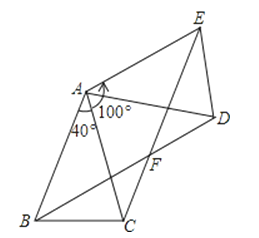
-
科目: 来源: 题型:
查看答案和解析>>【题目】把一副三角板如图甲放置,其中
 ,
,  ,斜边AB=6cm,DC=7cm把三角板DCE绕点C顺时针旋转15°得到△D1CE1(如图乙).这时AB与CD1相交于点O,与D1E1相交于点F .
,斜边AB=6cm,DC=7cm把三角板DCE绕点C顺时针旋转15°得到△D1CE1(如图乙).这时AB与CD1相交于点O,与D1E1相交于点F . 
(1)求 的度数;
的度数;
(2)求线段AD1的长;
(3)若把三角形D1CE1绕着点 C 顺时针再旋转30°得△D2CE2 , 这时点B在△D2CE2的内部、外部、还是边上?说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】四边形ABCD中,∠A=100°,∠C=70°.点M,N分别在AB,BC上,将△BMN沿MN翻折,得△FMN.若MF∥AD,FN∥DC,则∠D=_____°.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,AB=AC,把△ABC绕A点沿顺时针方向旋转得到△ADE,连接BD,CE交于点F.

(1)求证:△AEC≌△ADB;
(2)若AB=2,∠BAC=45°,当四边形ADFC是菱形时,求BF的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形
 中,
中, ,点
,点 是
是 上的一点,
上的一点, ,
, 的垂直平分线交
的垂直平分线交 的延长线于点
的延长线于点 ,连接
,连接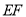 交
交 于点
于点 .若
.若 是
是 的中点,则
的中点,则 的长是________.
的长是________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,每个小正方形边长都为1个单位长度.

①画出将△ABC向下平移4个单位得到的△A1B1C1;
②画出△ABC关于原点O的中心对称图形△A2B2C2;
③画出△A1B1C1绕着点A1顺时针方向旋转90°后得到的△A3B3C3 .
相关试题

