【题目】如图,在直角坐标系中点A(2,0),点P在射线 ![]() (x<0)上运动,设点P的横坐标为a,以AP为直径作⊙C,连接OP、PB,过点P作PQ⊥OP交⊙C于点Q.
(x<0)上运动,设点P的横坐标为a,以AP为直径作⊙C,连接OP、PB,过点P作PQ⊥OP交⊙C于点Q.
(1)证明:∠AOP=∠BPQ;
(2)当点P在运动的过程中,线段PQ的长度是否发生变化,若变化,请用含a的代数式表示PQ的长;若不变,求出PQ的长;
(3)当tan∠APO= ![]() 时,①求点Q坐标;②点D是圆上任意一点,求QD+
时,①求点Q坐标;②点D是圆上任意一点,求QD+ ![]() OD的最小值.
OD的最小值.
参考答案:
【答案】
(1)解:由题意得点P(a,- ![]() a),∵AP为直径,∴∠PBA=90°,∴tan∠BOP=
a),∵AP为直径,∴∠PBA=90°,∴tan∠BOP= ![]() ,∴∠BPO=30°,∠POB=60°,∵PQ⊥OP,∴∠BPQ=∠AOP=120°
,∴∠BPO=30°,∠POB=60°,∵PQ⊥OP,∴∠BPQ=∠AOP=120°
(2)解:不变.如图1,连结BQ,
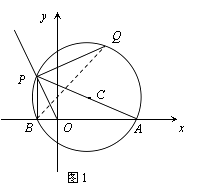
∵∠Q=∠PAO,∠BPQ=∠AOP,
∴△BPQ∽△POA.
∴ ![]() ,
,
∴PQ= ![]()
(3)解:①如图2,连结AQ,过点Q作QH⊥BP
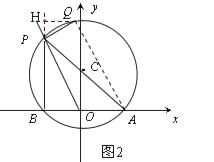
∵AP是直径,
∴∠PQA=90°.
∵∠OPQ=90°,
∴OP∥AQ.
∴∠OPA=∠PAQ,
∵tan∠OPA= ![]() ,
,
∴ ![]() ,
,
∵PQ= ![]() ,
,
∴AQ=5,AP=2 ![]() ,在RT△ABP中,AB=2-a,BP=-
,在RT△ABP中,AB=2-a,BP=- ![]() a,由(2-a)2+(
a,由(2-a)2+( ![]() a)2=(2
a)2=(2 ![]() )2,解得a1=-2,a2=3(舍去),
)2,解得a1=-2,a2=3(舍去),
∴P(-2,2 ![]() ),∠BPQ=120°,
),∠BPQ=120°,
∴∠HPQ=60°,
∴PH= ![]() ,HQ=
,HQ= ![]() ,
,
∴点Q(- ![]() ,
, ![]() );
);
②如图3,
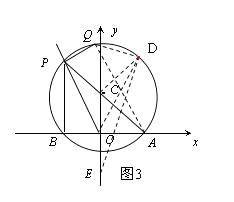
由①得CD= ![]() ,
,
∵P(-2,2 ![]() ),A(2,0),
),A(2,0),
∴C(0, ![]() ) ,OC=
) ,OC= ![]() ,在y轴上找点E使CE=
,在y轴上找点E使CE= ![]() ,
,
∴E(0,- ![]() ),
),
∴CD2=CO·CE,
∵∠DCO=∠ECD,
∴△DCO∽△ECD,
∴DE= ![]() OD,
OD,
∵QD+DE≥QE,
∴QD+ ![]() OD的最小值为
OD的最小值为 ![]()
【解析】(1)首先表示出P点的坐标,根据直径所对的圆周角是直角得出∠PBA=90°,根据正切三角函数的定义及特殊锐角三角函数值得出∠POB=60°,根据三角形的内角和得出∠BPO=30°,再根据垂直的定义得出∠BPQ=∠AOP=120°;
(2)不变.如图1,连结BQ,根据同弧所对的圆周角相等得出∠Q=∠PAO,又由(1)知∠BPQ=∠AOP,从而判断出△BPQ∽△POA,根据相似三角形对应边成比例得出答案;
(3)①如图2,连结AQ,过点Q作QH⊥BP,根据直径所对的圆周角是直角得出∠PQA=90°,然后根据同旁内角互补两直线平行得出OP∥AQ,根据平行线的性质得出∠OPA=∠PAQ,然后根据正切三角函数的定义打得出![]() =
=![]() ,从而得出AQ,AP的长,在Rt△ABP中,根据勾股定理得出关于a的方程,求出a的值,从而得出p点的坐标,进一步得出Q点的坐标;②如图3,由①得CD=
,从而得出AQ,AP的长,在Rt△ABP中,根据勾股定理得出关于a的方程,求出a的值,从而得出p点的坐标,进一步得出Q点的坐标;②如图3,由①得CD= ![]() ,由P,A两点的坐标得出C点的坐标及OC的长,在y轴上找点E使CE=
,由P,A两点的坐标得出C点的坐标及OC的长,在y轴上找点E使CE= ![]() ,进而得出E点坐标,从而得出CD2=CO·CE,然后判断出△DCO∽△ECD,根据相似三角形的性质得出DE=
,进而得出E点坐标,从而得出CD2=CO·CE,然后判断出△DCO∽△ECD,根据相似三角形的性质得出DE= ![]() OD,又因QD+DE≥QE,从而得出答案。
OD,又因QD+DE≥QE,从而得出答案。
【考点精析】认真审题,首先需要了解平行线的判定与性质(由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质),还要掌握圆周角定理(顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半)的相关知识才是答题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一个两位正整数m的个位数为8,则称m为“好数”.
(1)求证:对任意“好数”m,m2-64一定为20的倍数;
(2)若m=p2-q2,且p,q为正整数,则称数对(p,q)为“友好数对”,规定:
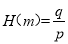 ,例如68=182-162,称数对(18,16)为“友好数对”,则
,例如68=182-162,称数对(18,16)为“友好数对”,则 ,求小于50的“好数”中,所有“友好数对”的H(m)的最大值.
,求小于50的“好数”中,所有“友好数对”的H(m)的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某市有一块长为(3a+b)米,宽为(2a+b)米的长方形地块,中间是边长为(a+b)米的正方形,规划部门计划将在中间的正方形修建一座雕像,四周的阴影部分进行绿化,
(1)绿化的面积是多少平方米?(用含字母a、b的式子表示)
(2)求出当a=20,b=12时的绿化面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC的外角∠ACD的平分线CP与内角∠ABC平分线BP交于点P,若∠BPC=40°,求∠CAB和∠CAP的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,O是△ABC的外心,OD⊥BC,OE⊥AC,OF⊥AB,则OD:OE:OF等于( ).

A.a:b:c
B.
C.sinA:sinB:sinC
D.cosA:cosB:cosC -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=ax2+bx+c(b>a>0)与x轴最多有一个交点,现有以下四个结论: ①该抛物线的对称轴在y轴左侧;
②关于x的方程ax2+bx+c+2=0无实数根;
③a﹣b+c≥0;
④ 的最小值为3.
的最小值为3.
其中,正确结论的个数为( )
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
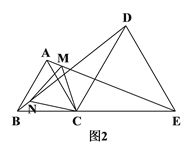
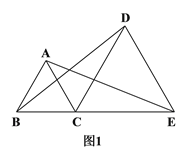
查看答案和解析>>【题目】如图1,C是线段BE上一点,以BC、CE为边分别在BE的同侧作等边△ABC和等边△DCE,连结AE、BD.
(1)求证:BD=AE;
(2)如图2,若M、N分别是线段AE、BD上的点,且AM=BN,请判断△CMN的形状,并说明理由.
相关试题

