【题目】若一个两位正整数m的个位数为8,则称m为“好数”.
(1)求证:对任意“好数”m,m2-64一定为20的倍数;
(2)若m=p2-q2,且p,q为正整数,则称数对(p,q)为“友好数对”,规定: ![]() ,例如68=182-162,称数对(18,16)为“友好数对”,则
,例如68=182-162,称数对(18,16)为“友好数对”,则![]() ,求小于50的“好数”中,所有“友好数对”的H(m)的最大值.
,求小于50的“好数”中,所有“友好数对”的H(m)的最大值.
参考答案:
【答案】(1)证明见解析;(2)![]() .
.
【解析】试题分析:
(1)设![]() 的十位数字为
的十位数字为![]() ,则由题意可得:
,则由题意可得: ![]() ,由此可得:
,由此可得: ![]() ,由此可得
,由此可得![]() 一定是20的倍数;
一定是20的倍数;
(2)设![]() 的十位数字为
的十位数字为![]() ,则由题意可得:
,则由题意可得: ![]() ,结合
,结合![]() ,且
,且![]() 为正整数及
为正整数及![]() 分
分![]() =1或2或3或4进行讨论求得符合条件的
=1或2或3或4进行讨论求得符合条件的![]() 的值,再求得对应的H(m)的值并比较大小即可求得本题答案.
的值,再求得对应的H(m)的值并比较大小即可求得本题答案.
试题解析:
(1)设![]() 的十位数字为
的十位数字为![]() ,则由题意可得:
,则由题意可得: ![]() ,
,
∴![]() ,
,
∵![]() 为两位正整数
为两位正整数![]() 的十位数字,
的十位数字,
∴![]() 是整数,
是整数,
∴![]() 是20的倍数;
是20的倍数;
(2)设![]() 的十位数字为
的十位数字为![]() ,则由题意可得:
,则由题意可得: ![]() ,
,
∵![]() ,且
,且![]() 为正整数,
为正整数,
∴![]() ,
,
又∵![]() ,
,
∴①当![]() 时,
时, ![]() ,此时没有满足条件的
,此时没有满足条件的![]() ;
;
②当![]() 时,
时, ![]() ,此时满足条件的
,此时满足条件的![]() 是数对(8,6),即
是数对(8,6),即![]() ,故H(28)=
,故H(28)=![]() ;
;
③当![]() 时,
时, ![]() ,此时没有满足条件的
,此时没有满足条件的![]() ;
;
④当![]() 时,
时, ![]() ,此时满足条件的
,此时满足条件的![]() 有数对(7,1)、(8,4)、(13,11),即
有数对(7,1)、(8,4)、(13,11),即![]() ,故H(48)=
,故H(48)=![]() 或H(48)=
或H(48)=![]() 或H(48)=
或H(48)=![]() ;
;
综上所述,∵![]() ,
,
∴小于50的“好数”中,所有“友好数对”的H(m)的最大值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】织里某品牌童装在甲、乙两家门店同时销售A,B两款童装,4月份甲门店销售A款童装60件,B款童装15件,两款童装的销售总额为3600元,乙门店销售A款童装40件,B款童装60件,两款童装的销售总额为4400元.
(1)A款童装和B款童装每件售价各是多少元?
(2)现计划5月将A款童装的销售额增加20%,问B款童装的销售额需增加百分之几,才能使A,B两款童装的销售额之比为4:3?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,大楼外墙有高为AB的广告牌,由距离大楼20米的点C(即CD=20米)观察它的顶部A的仰角是55°,底部B的仰角是42°,求AB的高度.(参考数据:sin55°≈0.82,cos55°≈0.57,tan55°≈1.43,sin42°≈0.67,cos42°≈0.74,tan42°≈0.90)

-
科目: 来源: 题型:
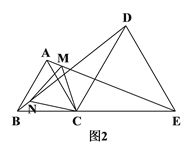
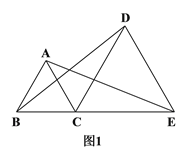
查看答案和解析>>【题目】如图1,C是线段BE上一点,以BC、CE为边分别在BE的同侧作等边△ABC和等边△DCE,连结AE、BD.
(1)求证:BD=AE;
(2)如图2,若M、N分别是线段AE、BD上的点,且AM=BN,请判断△CMN的形状,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义新运算:
 .
.例如:3
 2=3(3-2)=3,-1
2=3(3-2)=3,-1 4=-1
4=-1 (-1-4)=5.
(-1-4)=5.(1)请直接写出3
 a=b的所有正整数解;
a=b的所有正整数解;(2)已知2
 a=5b-2m,3
a=5b-2m,3 b=5a+m,说明:12a+11b的值与m无关;
b=5a+m,说明:12a+11b的值与m无关;(3)已知a>1,记M=ab
 b,N=b
b,N=b ab,试比较M,N的大小.
ab,试比较M,N的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校体育老师为了解该校八年级学生对球类运动项目的喜爱情况,进行了随机抽样调查(每位学生必须且只能选择一项最喜爱的运动项目),并将调查结果进行整理,绘制了如图不完整的统计图表.请根据图表中的信息解答下列问题:
类别
频数
A.乒乓球
16
B.足球
20
C.排球
n
D.篮球
15
E.羽毛球
m

(1)填空:m= , n=;
(2)若该年级有学生800人,请你估计这个年级最喜爱篮球的学生人数;
(3)在这次调查中随机抽中一名最喜爱足球的学生的概率是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知△BAD和△BCE均为等腰直角三角形,∠BAD=∠BCE=90°,点M为DE的中点.过点E与AD平行的直线交射线AM于点N.
(1)当A,B,C三点在同一直线上时(如图1),求证:M为AN的中点;
(2)将图1中△BCE绕点B旋转,当A,B,E三点在同一直线上时(如图2),求证:△CAN为等腰直角三角形;
(3)将图1中△BCE绕点B旋转到图3的位置时,(2)中的结论是否仍然成立?若成立,试证明之;若不成立,请说明理由.

相关试题

