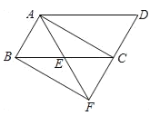
【题目】已知:如图,在□ABCD中,点E是BC的中点,连接AE并延长交DC的延长线于点F,连接BF.
(1)求证:△ABE≌△FCE;
(2)若AF=AD,判断四边形ABFC的形状,并说明理由.
参考答案:
【答案】(1)证明见解析;(2)四边形ABFC是矩形,证明见解析;
【解析】
(1)根据平行四边形的性质得出AB∥DC,推出![]() ,根据AAS证两三角形全等即可;
,根据AAS证两三角形全等即可;
(2)根据全等得出AB=CF,根据AB∥CF得出平行四边形ABFC,推出BC=AF,根据矩形的判定推出即可;
(1)证明:如图,

∵四边形ABCD是平行四边形,
∴AB ∥DC,即AB∥DF,
∴![]() ,
,
∵点E是BC的中点,
∴BE=EC,
在△ABE和△FCE中,
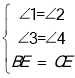 ,
,
∴![]() .
.
(2)四边形ABFC是矩形,理由如下:
∵![]() ,
,
∴AB=FC,
∵AB∥FC,
∴四边形ABFC是平行四边形,
∴AD=BC,
∵AF=AD,
∴AF=BC,
∴四边形ABFC是矩形.
-
科目: 来源: 题型:
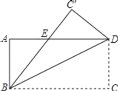
查看答案和解析>>【题目】如图,矩形ABCD沿着直线BD折叠,使点C落在C′处,BC′交AD于点E,AD=4,AB=3,求AE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,某工程队准备在山坡(山坡视为直线l)上修一条路,需要测量山坡的坡度,即tanα的值.测量员在山坡P处(不计此人身高)观察对面山顶上的一座铁塔,测得塔尖C的仰角为31°,塔底B的仰角为26.6°.已知塔高BC=40米,塔所在的山高OB=240米,OA=300米,图中的点O、B、C、A、P在同一平面内.
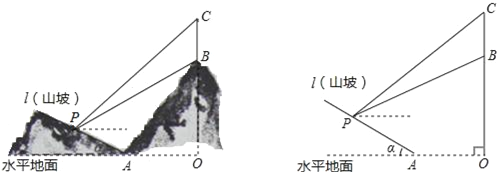
求:
(1)P到OC的距离.
(2)山坡的坡度tanα.
(参考数据sin26.6°≈0.45,tan26.6°≈0.50;sin31°≈0.52,tan31°≈0.60)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点O是直线AB上的一点,∠COD是直角,OE平分∠BOC.

(1)如图(1),若∠AOC=
 ,求∠DOE的度数;
,求∠DOE的度数;(2)如图(2),将∠COD绕顶点O旋转,且保持射线OC在直线AB上方,在整个旋转过程中,当∠AOC的度数是多少时,∠COE=2∠DOB.
-
科目: 来源: 题型:
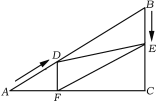
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,AB=60cm,∠A=30°,点D从点A出发沿AB方向以2cm/秒的速度向点B匀速运动,同时点E从点B出发沿BC方向以1cm/秒的速度向点C匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(0<t≤30).过点D作DF⊥AC于点F,连接DE,EF.
(1)填空:四边形BEFD是_________;
(2)当t=______时,四边形BEFD能够成为菱形。
(3)当t为何值时?△DEF为直角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD、正方形A1B1C1D1、正方形A2B2C2D2均位于第一象限内,它们的边平行于x轴或y轴,其中点A、A1、A2在直线OM上,点C、C1、C2在直线ON上,O为坐标原点,已知点A的坐标为(3,3),正方形ABCD的边长为1.若正方形A2B2C2D2的边长为2011,则点B2的坐标为___________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(背景知识)数轴是初中数学的一个重要工具,利用数轴可以将数与形完美地结合.研究数轴我们发现了许多重要的规律:若数轴上点A、点B表示的数分别为a、b,则A,B两点之间的距离AB=|a–b|,线段AB的中点表示的数为
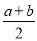 .
.(问题情境)如图,数轴上点A表示的数为–2,点B表示的数为8,点P从点A出发,以每秒3个单位长度的速度沿数轴向右匀速运动,同时点Q从点B出发,以每秒2个单位长度的速度向左匀速运动.
设运动时间为t秒(t>0).
(综合运用)(1)填空:①A、B两点间的距离AB=__________,线段AB的中点表示的数为__________;
②用含t的代数式表示:t秒后,点P表示的数为__________;点Q表示的数为__________.
(2)求当t为何值时,P、Q两点相遇,并写出相遇点所表示的数;
(3)求当t为何值时,PQ=
 AB;
AB;(4)若点M为PA的中点,点N为PB的中点,点P在运动过程中,线段MN的长度是否发生变化?若变化,请说明理由;若不变,请求出线段MN的长.
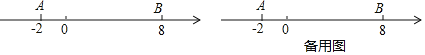
相关试题

