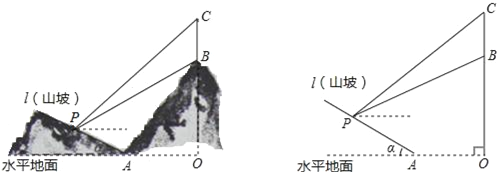
【题目】如图所示,某工程队准备在山坡(山坡视为直线l)上修一条路,需要测量山坡的坡度,即tanα的值.测量员在山坡P处(不计此人身高)观察对面山顶上的一座铁塔,测得塔尖C的仰角为31°,塔底B的仰角为26.6°.已知塔高BC=40米,塔所在的山高OB=240米,OA=300米,图中的点O、B、C、A、P在同一平面内.
求:
(1)P到OC的距离.
(2)山坡的坡度tanα.
(参考数据sin26.6°≈0.45,tan26.6°≈0.50;sin31°≈0.52,tan31°≈0.60)
参考答案:
【答案】(1)P到OC的距离为400米;(2)tanα=0.4
【解析】试题分析:(1)过点P作PD⊥OC于D,PE⊥OA于E,则四边形ODPE为矩形,先解Rt△PBD,得出BD=PDtan26.6°;解Rt△CPD,得出CD=PDtan31°;再根据CD﹣BD=BC,列出方程,求出PD=400即可求得点P到OC的距离;
(2)利用求得的线段PD的长求出PE=40,AE=100,然后在△APE中利用三角函数的定义即可求解.
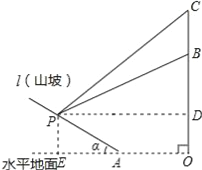
试题解析:(1)如图,过点P作PD⊥OC于D,PE⊥OA于E,则四边形ODPE为矩形.
在Rt△PBD中,∵∠BDP=90°,∠BPD=26.6°,
∴BD=PDtan∠BPD=PDtan26.6°;
在Rt△CPD中,∵∠CDP=90°,∠CPD=31°,
∴CD=PDtan∠CPD=PDtan31°;
∵CD﹣BD=BC,
∴PDtan31°﹣PDtan26.6°=40,
∴0.60PD﹣0.50PD=40,
解得PD=400(米),
∴P到OC的距离为400米;
(2)在Rt△PBD中,BD=PDtan26.6°≈400×0.50=200(米),
∵OB=240米,
∴PE=OD=OB﹣BD=40米,
∵OE=PD=400米,
∴AE=OE﹣OA=400﹣300=100(米),
∴tanα=![]() =0.4,
=0.4,
∴坡度为0.4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】针对动物园中四种可爱的动物:熊猫、孔雀、小猴、梅花鹿,想了解本班同学喜欢哪种动物的人最多,则调查对象是( )
A.本班全体同学
B.熊猫、孔雀、小猴、梅花鹿
C.记录下来的数据
D.同学们的选票 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,AB=5,AC=3,点D是BC上一动点,连结AD,将△ACD沿AD折叠,点C落在点C′,连结C′D交AB于点E,连结BC′.当△BC′D是直角三角形时,DE的长为_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算题 ——
(1)计算: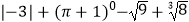
(2)已知: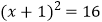 ,求
,求 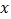 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,一次函数y=ax+b(a≠0)的图形与反比例函数y=
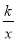 (k≠0)的图象交于第二、四象限内的A、B两点,与y轴交于C点,过点A作AH⊥y轴,垂足为H,OH=3,tan∠AOH=
(k≠0)的图象交于第二、四象限内的A、B两点,与y轴交于C点,过点A作AH⊥y轴,垂足为H,OH=3,tan∠AOH=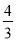 ,点B的坐标为(m,﹣2).
,点B的坐标为(m,﹣2).(1)求△AHO的周长;
(2)求该反比例函数和一次函数的解析式.

-
科目: 来源: 题型:
查看答案和解析>>【题目】动物园中有熊猫,孔雀,大象,梅花鹿四种可爱动物,为了解本班同学喜欢哪种动物的人最多,则调查的对象是( ).
A.本班的每一个同学
B.熊猫,孔雀,大象,梅花鹿
C.同学们的选票
D.记录下来的数据 -
科目: 来源: 题型:
查看答案和解析>>【题目】若3x+2y2=0,则8x4y等于____.
相关试题

