【题目】如图,正方形ABCD、正方形A1B1C1D1、正方形A2B2C2D2均位于第一象限内,它们的边平行于x轴或y轴,其中点A、A1、A2在直线OM上,点C、C1、C2在直线ON上,O为坐标原点,已知点A的坐标为(3,3),正方形ABCD的边长为1.若正方形A2B2C2D2的边长为2011,则点B2的坐标为___________.

参考答案:
【答案】(4022,6033)
【解析】
根据已知条件可求得点B和点C的坐标,令直线ON的表达式为y=kx,代入A得坐标,可求得k,即得出直线ON的表达式,再根据已知条件求出点B2的值.
设直线OM的解析式为![]() ,
,
已知点A、![]() 、
、![]() 在直线OM上且
在直线OM上且![]() ,
,
把点A代入可得OM的解析式为![]() ,
,
正方形ABXD的边长为1,所以B点的坐标为![]() ,则点C的坐标为
,则点C的坐标为![]() ,
,
∵点C、![]() 、
、![]() 在直线ON上,可解得直线ON的解析式为
在直线ON上,可解得直线ON的解析式为![]() ,
,
设![]() 的坐标为
的坐标为![]() ,
,
∵点![]() 在直线ON上,
在直线ON上,
∴![]() ,
,
∵正方形![]() D的边长为2011,
D的边长为2011,
∴![]() 的坐标为
的坐标为![]() ,
,![]() 的坐标为
的坐标为![]() ,
,
∵点![]() 在直线OM上,则
在直线OM上,则![]() ,
,
则![]() ,
,
∴![]() 。
。
解得![]() .
.
则点![]() 的坐标为(4022,6033).
的坐标为(4022,6033).
故答案为(4022,6033).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点O是直线AB上的一点,∠COD是直角,OE平分∠BOC.

(1)如图(1),若∠AOC=
 ,求∠DOE的度数;
,求∠DOE的度数;(2)如图(2),将∠COD绕顶点O旋转,且保持射线OC在直线AB上方,在整个旋转过程中,当∠AOC的度数是多少时,∠COE=2∠DOB.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在□ABCD中,点E是BC的中点,连接AE并延长交DC的延长线于点F,连接BF.
(1)求证:△ABE≌△FCE;
(2)若AF=AD,判断四边形ABFC的形状,并说明理由.
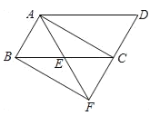
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,AB=60cm,∠A=30°,点D从点A出发沿AB方向以2cm/秒的速度向点B匀速运动,同时点E从点B出发沿BC方向以1cm/秒的速度向点C匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(0<t≤30).过点D作DF⊥AC于点F,连接DE,EF.
(1)填空:四边形BEFD是_________;
(2)当t=______时,四边形BEFD能够成为菱形。
(3)当t为何值时?△DEF为直角三角形.
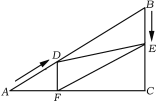
-
科目: 来源: 题型:
查看答案和解析>>【题目】(背景知识)数轴是初中数学的一个重要工具,利用数轴可以将数与形完美地结合.研究数轴我们发现了许多重要的规律:若数轴上点A、点B表示的数分别为a、b,则A,B两点之间的距离AB=|a–b|,线段AB的中点表示的数为
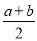 .
.(问题情境)如图,数轴上点A表示的数为–2,点B表示的数为8,点P从点A出发,以每秒3个单位长度的速度沿数轴向右匀速运动,同时点Q从点B出发,以每秒2个单位长度的速度向左匀速运动.
设运动时间为t秒(t>0).
(综合运用)(1)填空:①A、B两点间的距离AB=__________,线段AB的中点表示的数为__________;
②用含t的代数式表示:t秒后,点P表示的数为__________;点Q表示的数为__________.
(2)求当t为何值时,P、Q两点相遇,并写出相遇点所表示的数;
(3)求当t为何值时,PQ=
 AB;
AB;(4)若点M为PA的中点,点N为PB的中点,点P在运动过程中,线段MN的长度是否发生变化?若变化,请说明理由;若不变,请求出线段MN的长.
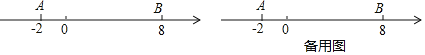
-
科目: 来源: 题型:
查看答案和解析>>【题目】下图中的程序表示,输入一个整数
 便会按程序进行计算.
便会按程序进行计算.
设输入的
 值为
值为 ,那么根据程序,第
,那么根据程序,第 次计算的结果是
次计算的结果是 ;第
;第 次计算的结果是
次计算的结果是 ,这样下去第5次计算的结果是__________,第2019次计算的结果是______________.
,这样下去第5次计算的结果是__________,第2019次计算的结果是______________. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠ACB=90°,sinA=
 ,BC=8,点D是AB的中点,过点B作CD的垂线,垂足为点E.
,BC=8,点D是AB的中点,过点B作CD的垂线,垂足为点E.(1)求线段CD的长;
(2)求cos∠ABE的值。

相关试题

