【题目】阅读下列材料:
已知:如图1,等边△A1A2A3内接于⊙O,点P是![]() 上的任意一点,连接PA1,PA2,PA3,可证:PA1+PA2=PA3,从而得到:
上的任意一点,连接PA1,PA2,PA3,可证:PA1+PA2=PA3,从而得到:![]() 是定值.
是定值.
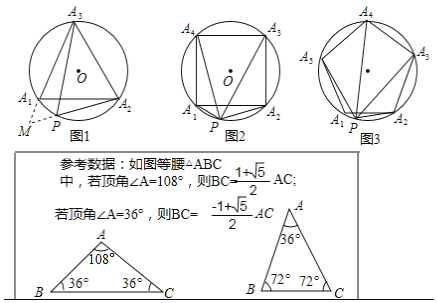
(1)以下是小红的一种证明方法,请在方框内将证明过程补充完整;
证明:如图1,作∠PA1M=60°,A1M交A2P的延长线于点M.
∵△A1A2A3是等边三角形,
∴∠A3A1A2=60°,
∴∠A3A1P=∠A2A1M
又A3A1=A2A1,∠A1A3P=∠A1A2P,
∴△A1A3P≌△A1A2M

∴PA3=MA2=PA2+PM=PA2+PA1.
∴![]() ,是定值.
,是定值.
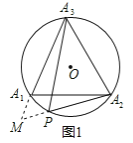
(2)延伸:如图2,把(1)中条件“等边△A1A2A3”改为“正方形A1A2A3A4”,其余条件不变,请问:![]() 还是定值吗?为什么?
还是定值吗?为什么?
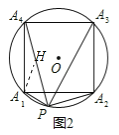
(3)拓展:如图3,把(1)中条件“等边△A1A2A3”改为“正五边形A1A2A3A4A5”,其余条件不变,则![]() = (只写出结果).
= (只写出结果).
参考答案:
【答案】(1)证明见解析;(2)是定值,理由见解析;(3)![]()
【解析】(2)结论:![]() 是定值.在A4P上截取AH=A2P,连接HA1.证明PA4=A4+PH=PA2+
是定值.在A4P上截取AH=A2P,连接HA1.证明PA4=A4+PH=PA2+![]() PA1,同法可证:PA3=PA1+
PA1,同法可证:PA3=PA1+![]() PA2,推出(
PA2,推出(![]() +1)(PA1+PA2)=PA3+PA4,可得PA1+PA2=(
+1)(PA1+PA2)=PA3+PA4,可得PA1+PA2=(![]() -1)(PA3+PA4),即可解决问题;
-1)(PA3+PA4),即可解决问题;
(3)结论:则![]() .如图3-1中,延长PA1到H,使得A1H=PA2,连接A4H,A4A2,A4A1.由△HA4A1≌△PA4A2,可得△A4HP是顶角为36°的等腰三角形,推出PH=
.如图3-1中,延长PA1到H,使得A1H=PA2,连接A4H,A4A2,A4A1.由△HA4A1≌△PA4A2,可得△A4HP是顶角为36°的等腰三角形,推出PH=![]() PA4,即PA1+PA2=
PA4,即PA1+PA2=![]() PA4,如图3-2中,延长PA5到H,使得A5H=PA3.同法可证:△A4HP是顶角为108°的等腰三角形,推出PH=
PA4,如图3-2中,延长PA5到H,使得A5H=PA3.同法可证:△A4HP是顶角为108°的等腰三角形,推出PH=![]() PA4,即PA5+PA3=
PA4,即PA5+PA3=![]() PA4,即可解决问题;
PA4,即可解决问题;
(1)如图1,作∠PA1M=60°,A1M交A2P的延长线于点M.
∵△A1A2A3是等边三角形,
∴∠A3A1A2=60°,
∴∠A3A1P=∠A2A1M
又A3A1=A2A1,∠A1A3P=∠A1A2P,
∴△A1A3P≌△A1A2M
∴PA3=MA2,
∵PM=PA1,
∴PA3=MA2=PA2+PM=PA2+PA1.
∴![]() ,是定值.
,是定值.
(2)结论:![]() 是定值.
是定值.
理由:在A4P上截取AH=A2P,连接HA1.
∵四边形A1A2A3A4是正方形,
∴A4A1=A2A1,
∵∠A1A4H=∠A1A2P,A4H=A2P,
∴△A1A4H=△A1A2P,
∴A1H=PA1,∠A4A1H=∠A2A1P,
∴∠HA1P=∠A4A1A2=90°
∴△HA1P的等腰直角三角形,
∴PA4=HA4+PH=PA2+![]() PA1,
PA1,
同法可证:PA3=PA1+![]() PA2,
PA2,
∴(![]() +1)(PA1+PA2)=PA3+PA4,
+1)(PA1+PA2)=PA3+PA4,
∴PA1+PA2=(![]() -1)(PA3+PA4),
-1)(PA3+PA4),
∴![]() .
.
(3)结论:则![]() .
.
理由:如图3-1中,延长PA1到H,使得A1H=PA2,连接A4H,A4A2,A4A1.
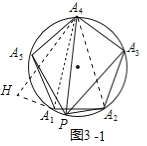
由△HA4A1≌△PA4A2,可得△A4HP是顶角为36°的等腰三角形,
∴PH=![]() PA4,即PA1+PA2=
PA4,即PA1+PA2=![]() PA4,
PA4,
如图3-2中,延长PA5到H,使得A5H=PA3.
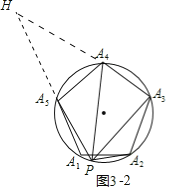
同法可证:△A4HP是顶角为108°的等腰三角形,
∴PH=![]() PA4,即PA5+PA3=
PA4,即PA5+PA3=![]() PA4,
PA4,
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若规定
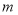 ,
,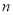 两数之间满足一种运算。 记作
两数之间满足一种运算。 记作 ,若
,若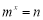 ,则
,则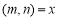 .我们叫这样的数对称为“一青一对”。例如:因为
.我们叫这样的数对称为“一青一对”。例如:因为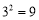 .所以
.所以
(1)根据上述规定要求,请完成填空:
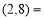 ________.
________. 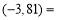 ________.
________. 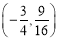 __________
__________(2)计算
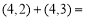 (___________)并写出计算过程
(___________)并写出计算过程(3)在正整数指数幂的范围内,若
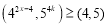 恒成立, 且
恒成立, 且 只有两个正整数解,求
只有两个正整数解,求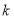 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知在平面直角坐标系中,点
 的坐标是
的坐标是 ,点
,点 是第一象限内一动点。
是第一象限内一动点。(1) ①:如图①.若动点
 满足
满足 ,且
,且 ,求点
,求点 的坐标。
的坐标。②:如图②,在第(1)问的条件下,将
 逆时针旋转至如图
逆时针旋转至如图 所示位置,求
所示位置,求 的值.
的值.(2)如图③,若点
 与点
与点 关于轴对称,且
关于轴对称,且 , 若动点
, 若动点 满足
满足 ',问:
',问: 的值是否发生变化?若变化,请说明理由,若不变化,请求出其值。
的值是否发生变化?若变化,请说明理由,若不变化,请求出其值。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于E,AD⊥CE于D.

(1)求证:△ADC≌△CEB.
(2)AD=5cm,DE=3cm,求BE的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB=AC,AD=AE,,若要得到△ABD≌△ACE,必须添加一个条件,则下列所添条件不恰当的是 ( ).

A. BD=CEB. ∠ABD=∠ACEC. ∠BAD=∠CAED. ∠BAC=∠DAE
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知下列结论:①若
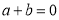 ,则
,则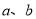 互为相反数;②若
互为相反数;②若 ,则
,则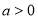 且
且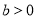 ;③
;③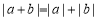 ;④绝对值小于10的所有整数之和等于0;⑤3与-5是同类项.其中正确的结论有( )个.
;④绝对值小于10的所有整数之和等于0;⑤3与-5是同类项.其中正确的结论有( )个.A.2B.3C.4D.5
-
科目: 来源: 题型:
查看答案和解析>>【题目】在数学课上,林老师在黑板上画出如图所示的图形(其中点B、F、C、E在同一直线上),并写出四个条件:①AB=DE,②BF=EC,③∠B=∠E,④∠1=∠2.请你从这四个条件中选出三个作为题设,另一个作为结论,组成一个真命题,并给予证明.题设:______________;结论:________.(均填写序号)
证明:

相关试题

