Question

【题目】在平面直角坐标系中的位置如图所示．

（1）作出关于轴对称的，并写出各顶点的坐标；

（2）将向右平移6个单位，作出平移后的并写出各顶点的坐标；

（3）观察和，它们是否关于某直线对称？若是，请用粗线条画出对称轴．

Answer 1

【答案】（1）图见解析；点，点，点；（2）图见解析；点，点，点；（3）是，图见解析

【解析】

（1）先找到A、B、C关于y轴的对称点，然后连接、、即可，然后根据平面直角坐标系写出A、B、C的坐标，根据关于y轴对称的两点坐标关系：横坐标互为相反数，纵坐标相等即可写出的坐标；

（2）先分别将A、B、C向右平移6个单位，得到，然后连接、、即可，然后根据平移的坐标规律：横坐标左减右加即可写出的坐标；

（3）根据两个图形成轴对称的定义，画出对称轴即可．

解：（1）先找到A、B、C关于y轴的对称点，然后连接、、，如图所示：即为所求，

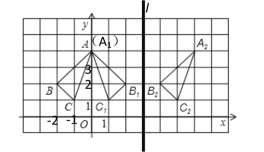
由平面直角坐标系可知：点A（0,4），点B（-2，2），点C（-1，1）

∴点，点，点；

（2）先分别将A、B、C向右平移6个单位，得到，然后连接、、，如图所示：即为所求，

∵点A（0,4），点B（-2，2），点C（-1，1）

∴点，点，点；

（3）如图所示，和关于直线l对称，所以直线l即为所求．