【题目】如图1,平面直角坐标系中,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() ,
,![]() ,直线
,直线![]() 经过点
经过点![]() ,并与
,并与![]() 轴交于点
轴交于点![]() .
.
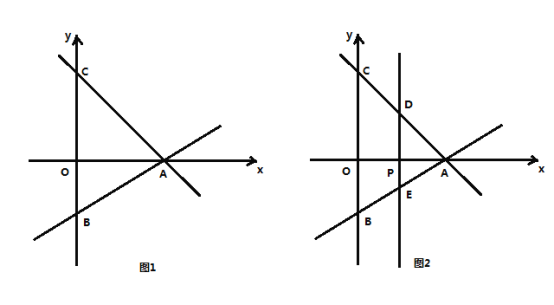
(1)求![]() ,
,![]() 两点的坐标及
两点的坐标及![]() 的值;
的值;
(2)如图2,动点![]() 从原点
从原点![]() 出发,以每秒
出发,以每秒![]() 个单位长度的速度沿
个单位长度的速度沿![]() 轴正方向运动.过点
轴正方向运动.过点![]() 作
作![]() 轴的垂线,分别交直线
轴的垂线,分别交直线![]() ,
,![]() 于点
于点![]() ,
,![]() .设点
.设点![]() 运动的时间为
运动的时间为![]() .
.
①点![]() 的坐标为______.点
的坐标为______.点![]() 的坐标为_______;(均用含
的坐标为_______;(均用含![]() 的式子表示)
的式子表示)
②请从下面A、B两题中任选一题作答我选择________题.
A.当点![]() 在线段
在线段![]() 上时,探究是否存在某一时刻,使
上时,探究是否存在某一时刻,使![]() ?若存在,求出此时
?若存在,求出此时![]() 的面积;若不存在说明理由.
的面积;若不存在说明理由.
B.点![]() 是线段
是线段![]() 上一点.当点
上一点.当点![]() 在射线
在射线![]() 上时,探究是否存在某一时刻使
上时,探究是否存在某一时刻使![]() ?若存在、求出此时
?若存在、求出此时![]() 的值,并直接写出此时
的值,并直接写出此时![]() 为等腰三角形时点
为等腰三角形时点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
参考答案:
【答案】(1)点![]() 的坐标为
的坐标为![]() ,点B的坐标为
,点B的坐标为![]() ,
,![]() ;(2)①
;(2)①![]() ;
;![]() ;②A.
;②A.![]() ;B.点
;B.点![]() 的坐标为
的坐标为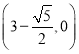 或
或![]() 或
或![]() 或
或![]() .
.
【解析】
(1)根据一次函数与坐标轴的交点坐标特点即可求出![]() ,
,![]() 两点的坐标,把
两点的坐标,把![]() 点坐标代入
点坐标代入![]() 即可求出b;
即可求出b;
(2)①依题意得P(t,0),把x=t分别代入直线![]() ,
,![]() 即可表示出D,E的坐标;
即可表示出D,E的坐标;
②A,根据![]() =2,即可求出t,得到
=2,即可求出t,得到![]() ,利用
,利用![]() 即可求解;
即可求解;
B,分当点![]() 在线段
在线段![]() 上时和当点
上时和当点![]() 在线段
在线段![]() 的延长线上时分别表示出DE,根据
的延长线上时分别表示出DE,根据![]() 求出t,再根据等腰三角形的性质即可求出
求出t,再根据等腰三角形的性质即可求出![]() 点坐标.
点坐标.
(1)将![]() 代入
代入![]() 得
得![]() ,
,
解,得![]() ,
,
![]() 点
点![]() 的坐标为
的坐标为![]() .
.
将![]() 代入
代入![]() 得
得![]() ,
,
![]() 点B的坐标为
点B的坐标为![]() .
.
将![]() 代入
代入![]() ,得
,得![]()
解,得![]() .
.
(2)①依题意得P(t,0),把x=t分别代入直线![]() ,
,![]()
得 ![]() ;
;![]()
故答案为![]() ;
;![]() .
.
②A.由①得![]() ,
,![]() ,
,
![]() 点
点![]() 在线段
在线段![]() 上,
上,
![]() ,
,
![]() ,
,![]() .
.
![]() ,
,![]() ,
,
解,得![]() .
.
![]() ,
,
![]() .
.
B.由①得![]() ,
,![]() .
.
![]() ,
,![]() .
.
当点![]() 在线段
在线段![]() 上时,
上时,
![]() ,
,
![]() ,
,
解得![]() .
.
∴P(3,0),D(3,1),E(3,-![]() )
)
设Q(a,0)(0≤a≤4)
故QD2=![]() ,QE2=
,QE2=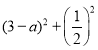 ,DE=
,DE=![]()
∵![]() 为等腰三角形
为等腰三角形
∴QD2=DE2或QE2=DE2
即![]() =
=![]() 或
或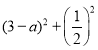 =
=![]()
解得a=![]() ,(a=
,(a=![]() 舍去)或a=
舍去)或a=![]() ,( a=
,( a=![]() 舍去)
舍去)
∴点![]() 的坐标为
的坐标为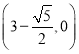 或
或![]() .
.
当点![]() 在线段
在线段![]() 的延长线上时,
的延长线上时,
![]()
![]() ,
,
解得![]() .
.
∴P(6,0),D(6,-2),E(6,1)
设Q(a,0)(0≤a≤4)
故QD2=![]() ,QE2=
,QE2=![]() ,DE=3
,DE=3
∵![]() 为等腰三角形
为等腰三角形
∴QD2=DE2或QE2=DE2
即![]() =9或
=9或![]() =9
=9
解得a=6-![]() ,(a=6+
,(a=6+![]() 舍去)或a=6-2
舍去)或a=6-2![]() ,( a=6+2
,( a=6+2![]() 舍去)
舍去)
点![]() 的坐标为
的坐标为![]() 或
或![]() .
.
综上所述,点![]() 的坐标为
的坐标为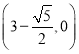 或
或![]() 或
或![]() 或
或![]() .
.
-
科目: 来源: 题型:
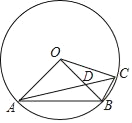
查看答案和解析>>【题目】如图,⊙O是△ABC的外接圆,OA=2cm,OA⊥OB,AC交OB于D点,AD=2CD.
(1)求∠BOC的度数;
(2)求线段BD、线段CD和 BC围成的图形的面积.
-
科目: 来源: 题型:
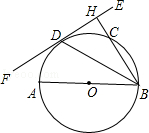
查看答案和解析>>【题目】如图,AB为⊙O的直径,EF切⊙O于点D,过点B作BH⊥EF于点H,交⊙O于点C,连接BD.
(1)求证:BD平分∠ABH;
(2)如果AB=12,BC=8,求圆心O到BC的距离.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在下列条件中,不能证明△ABD≌△ACD的是( ).

A.BD=DC, AB=AC B.∠ADB=∠ADC,BD=DC
C.∠B=∠C,∠BAD=∠CAD D. ∠B=∠C,BD=DC
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,BP平分∠ABC,D为BP上一点,E,F分别在BA,BC上,且满足DE=DF,若∠BED=140°,则∠BFD的度数是( )

A. 40°B. 50°C. 60°D. 70°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB为⊙O的直径,C,E为O上的两点,若AC平分∠EAB,CD⊥AE于点D.
(1)求证:DC是⊙O切线;
(2)若AO=6,DC=3
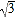 ,求DE的长;
,求DE的长;(3)过点C作CF⊥AB于F,如图2,若AD﹣OA=1.5,AC=3
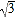 ,求图中阴影部分面积.
,求图中阴影部分面积.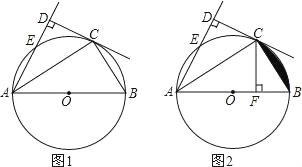
相关试题

