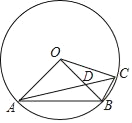
【题目】如图,⊙O是△ABC的外接圆,OA=2cm,OA⊥OB,AC交OB于D点,AD=2CD.
(1)求∠BOC的度数;
(2)求线段BD、线段CD和 BC围成的图形的面积.
参考答案:
【答案】(1) 30°;(2) 弧BC, ![]() .
.
【解析】
(1)作OF⊥AC于F,如图,设CD=x,则AD=2x,利用等腰三角形性质得AF=![]() x,则DF=
x,则DF=![]() x,再证明△AOF∽△ODF,利用相似比得到OF=
x,再证明△AOF∽△ODF,利用相似比得到OF=![]() x,则利用三角函数可求出∠OAF=30°,从而得到∠BOC的度数;
x,则利用三角函数可求出∠OAF=30°,从而得到∠BOC的度数;
(2)利用含30度的直角三角形三边的关系得到OF=1,AF=![]() ,则AC=2
,则AC=2![]() ,所以CD=
,所以CD=![]() ,然后根据三角形面积公式和扇形面积公式,利用线段BD、线段CD和弧BC围成的图形的面积=S扇形BOC-S△ODC进行计算.
,然后根据三角形面积公式和扇形面积公式,利用线段BD、线段CD和弧BC围成的图形的面积=S扇形BOC-S△ODC进行计算.
解:(1)作OF⊥AC于F,如图,设CD=x,则AD=2x,
∵OA=OC,
∴AF=![]() AC=
AC=![]() x,
x,
∴DF=2x﹣![]() x=
x=![]() x,
x,
∵OA⊥OB,
∴∠AOB=90°,
∴△AOF∽△ODF,
∴OF2=AFDF=![]() x
x![]() x,
x,
∴OF=![]() x,
x,
在Rt△OAF中,tan∠OAF=![]() =
=![]() =
=![]() ,
,
∴∠OAF=30°,
∴∠AOC=120°,
∴∠BOC=120°﹣90°=30°;
(2)∵OA=2,
∴OF=1,AF=![]() ,
,
∴AC=2![]() ,
,
∴CD=![]() AC=
AC=![]() ,
,
∴线段BD、线段CD和弧BC围成的图形的面积=S扇形BOC﹣S△ODC=![]() ﹣
﹣![]()
![]() 1=
1=![]() .
.
-
科目: 来源: 题型:
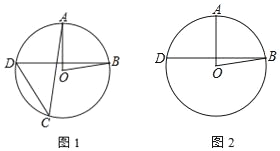
查看答案和解析>>【题目】如图,在⊙O中,半径OA与弦BD垂直,点C在⊙O上,∠AOB=80°
(1)若点C在优弧BD上,求∠ACD的大小;
(2)若点C在劣弧BD上,直接写出∠ACD的大小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个有进水管与出水管的容器,从某时刻开始
 分钟内只进水不出水.在随后的
分钟内只进水不出水.在随后的 分钟内既进水又出水,直到容器内的水量达到
分钟内既进水又出水,直到容器内的水量达到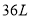 .如图,坐标系中的折线段
.如图,坐标系中的折线段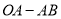 表示这一过程中容器内的水量
表示这一过程中容器内的水量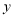 (单位:
(单位: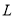 )与时间
)与时间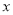 (单位:分)之间的关系.
(单位:分)之间的关系.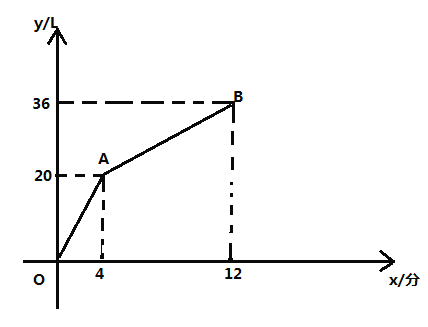
(1)单独开进水管,每分钟可进水________
 ;
;(2)求进水管与出水管同时打开时容器内的水量
 与时间
与时间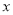 的函数关系式
的函数关系式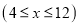 ;
;(3)当容器内的水量达到
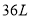 时,立刻关闭进水管,直至容器内的水全部放完.请在同一坐标系中画出表示放水过程中容器内的水量
时,立刻关闭进水管,直至容器内的水全部放完.请在同一坐标系中画出表示放水过程中容器内的水量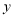 与时间
与时间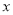 关系的线段
关系的线段 ,并直接写出点
,并直接写出点 的坐标.
的坐标. -
科目: 来源: 题型:
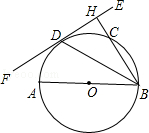
查看答案和解析>>【题目】如图,AB为⊙O的直径,EF切⊙O于点D,过点B作BH⊥EF于点H,交⊙O于点C,连接BD.
(1)求证:BD平分∠ABH;
(2)如果AB=12,BC=8,求圆心O到BC的距离.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,平面直角坐标系中,直线
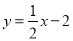 与
与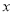 轴、
轴、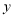 轴分别交于点
轴分别交于点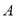 ,
,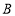 ,直线
,直线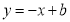 经过点
经过点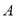 ,并与
,并与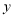 轴交于点
轴交于点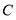 .
.
(1)求
 ,
, 两点的坐标及
两点的坐标及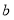 的值;
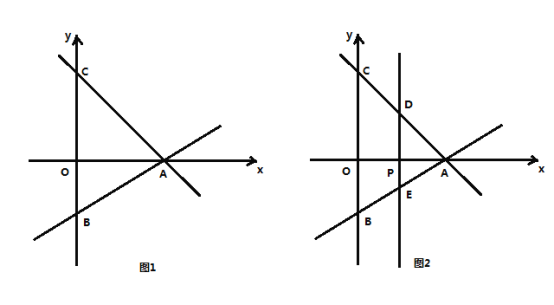
的值;(2)如图2,动点
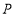 从原点
从原点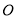 出发,以每秒
出发,以每秒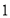 个单位长度的速度沿
个单位长度的速度沿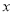 轴正方向运动.过点
轴正方向运动.过点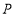 作
作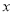 轴的垂线,分别交直线
轴的垂线,分别交直线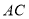 ,
,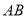 于点
于点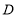 ,
,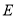 .设点
.设点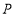 运动的时间为
运动的时间为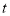 .
.①点
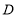 的坐标为______.点
的坐标为______.点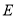 的坐标为_______;(均用含
的坐标为_______;(均用含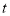 的式子表示)
的式子表示)②请从下面A、B两题中任选一题作答我选择________题.
A.当点
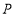 在线段
在线段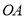 上时,探究是否存在某一时刻,使
上时,探究是否存在某一时刻,使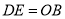 ?若存在,求出此时
?若存在,求出此时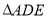 的面积;若不存在说明理由.
的面积;若不存在说明理由.B.点
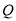 是线段
是线段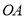 上一点.当点
上一点.当点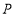 在射线
在射线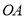 上时,探究是否存在某一时刻使
上时,探究是否存在某一时刻使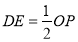 ?若存在、求出此时
?若存在、求出此时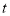 的值,并直接写出此时
的值,并直接写出此时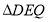 为等腰三角形时点
为等腰三角形时点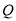 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在下列条件中,不能证明△ABD≌△ACD的是( ).

A.BD=DC, AB=AC B.∠ADB=∠ADC,BD=DC
C.∠B=∠C,∠BAD=∠CAD D. ∠B=∠C,BD=DC
相关试题

