【题目】如图,P为等边三角形ABC内的一点,且P到三个顶点A,B,C的距离分别为3,4,5,则△ABC的面积为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
参考答案:
【答案】A
【解析】将△BPC绕点B逆时针旋转60°得△BEA,根据旋转的性质得BE=BP=4,AE=PC=5,∠PBE=60°,则△BPE为等边三角形,得到PE=PB=4,∠BPE=60°,在△AEP中,AE=5,延长BP,作AF⊥BP于点F.AP=3,PE=4,根据勾股定理的逆定理可得到△APE为直角三角形,且∠APE=90°,即可得到∠APB的度数,在直角△APF中利用三角函数求得AF和PF的长,则在直角△ABF中利用勾股定理求得AB的长,进而求得三角形ABC的面积.
∵△ABC为等边三角形,
∴BA=BC,
可将△BPC绕点B逆时针旋转60°得△BEA,连EP,且延长BP,作AF⊥BP于点F.如图,
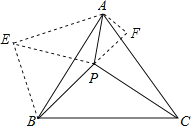
∴BE=BP=4,AE=PC=5,∠PBE=60°,
∴△BPE为等边三角形,
∴PE=PB=4,∠BPE=60°,
在△AEP中,AE=5,AP=3,PE=4,
∴AE2=PE2+PA2,
∴△APE为直角三角形,且∠APE=90°,
∴∠APB=90°+60°=150°.
∴∠APF=30°,
∴在直角△APF中,AF=![]() AP=
AP=![]() ,PF=
,PF=![]() AP=
AP=![]() .
.
∴在直角△ABF中,AB2=BF2+AF2=(4+![]() )2+(
)2+(![]() )2=25+12
)2=25+12![]() .
.
则△ABC的面积是![]() AB2=
AB2=![]() (25+12
(25+12![]() )=9+
)=9+![]() .
.
故选:A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】完成下面的证明过程:
已知:如图,
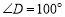 ,
,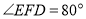 ,
,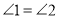 .
.求证:
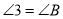 .
.
证明:∵
 ,
, (已知)
(已知)∴
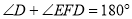 .
.∴
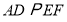 ,( )
,( )又∵
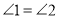 ,(已知)
,(已知)∴______
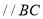 ,(内错角相等,两直线平行)
,(内错角相等,两直线平行)∴
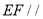 _______,( )
_______,( )∴
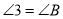 .( )
.( ) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC的两边AB和AC的垂直平分线分别交BC于D,E,若∠BAC+∠DAE=150°,则∠BAC的度数是( )
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】“校本课程”是学生课外活动的重要内容,某校共有“文学欣赏”、“英语角”、“趣味数学”、“法律普及”这四种校本课程.为了解学生参加“文学欣赏”、“英语角”、“趣味数学”、“法律普及”校本课程(以下分别用A、B、C、D表示)的情况,对学生进行了抽样调查,并将调查情况绘制成两幅统计图(尚不完整).

请根据以上信息,解答下列问题:
(1)本次抽样调查的学生共有人.
(2)将两幅统计图补充完整;
(3)若该校有4000人,请估计参加法律普及的人数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如果两个角的差的绝对值等于90°,就称这两个角互为垂角,其中一个角叫另一个角的垂角.
(1)如图1,O为直线AB上一点,∠AOC=90°,∠EOD=90°,直接写出图中∠BOE的垂角为 ;
(2)如果一个角的垂角等于这个角的补角的
 ,求这个角的度数;
,求这个角的度数;(3)如图2,O为直线AB上一点,∠AOC=75°,将整个图形绕点O逆时针旋转n°(0<n<180),直线AB旋转到A1B1,OC旋转到OC1,作射线OP,使∠BOP=
 ∠BOB′,试直接写出当n= 时,∠POA1与∠AOC1互为垂角.
∠BOB′,试直接写出当n= 时,∠POA1与∠AOC1互为垂角.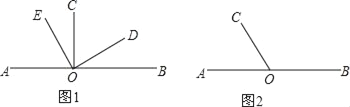
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC中,AB=41,AC=15,高AH=9,则△ABC的面积是________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,边AB、AC的垂直平分线分别交BC于D、E.
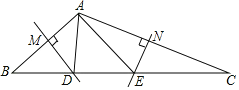
(1)若BC=8,则△ADE周长是多少?
(2)若∠BAC=118°,则∠DAE的度数是多少?
相关试题

