【题目】阅读下面一段文字:问题:![]() 能化为分数形式吗?
能化为分数形式吗?
探求:步骤①设![]() ,步骤②
,步骤②![]() ,
,
步骤③![]() ,则
,则![]() ,
,
步骤④![]() ,解得
,解得![]() .
.
根据你对这段文字的理解,回答下列问题:
(1)步骤①到步骤②的依据是____________;
(2)仿照上述探求过程,请你尝试把![]() 化为分数形式;
化为分数形式;
步骤①设![]() ,步骤②
,步骤②![]() ,
,
步骤③__________________,
步骤④____________,解得![]() ____________;
____________;
(3)请你将![]() 化为分数形式,并说明理由。
化为分数形式,并说明理由。
参考答案:
【答案】(1)等式的基本性质2;(2)![]() ,则
,则![]() ;100x=37+x,x=
;100x=37+x,x=![]() ;(3)
;(3)![]() ,理由见解析.
,理由见解析.
【解析】
(1)利用等式的基本性质得出答案;
(2)仿照材料中的探求过程,即可得出答案;
(3)利用已知设![]() ,进而得出10x=8+x,求出x=
,进而得出10x=8+x,求出x=![]() .再设
.再设![]() ,则
,则![]() =3+
=3+![]() =
=![]() ,求出m=
,求出m=![]() .
.
解:(1)步骤①到步骤②的依据是等式的基本性质2.
故答案为:等式的基本性质2;
(2)把![]() 化为分数形式:
化为分数形式:
步骤①设![]() ,步骤②
,步骤②![]() ,
,
步骤③![]() ,则
,则![]() ;
;
步骤④100x=37+x,解得x=![]() .
.
(3)设![]() ,10x=8+x,
,10x=8+x,
![]() ,
,![]() ,
,
10x=8+x,
解得:![]() .
.
设![]() ,
,
![]() ,
,
![]() ,
,
即![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰三角形ABC中,AB=AC=5cm,BC=8cm,动点N从点C出发,沿线段CB以2cm/s的速度向点B运动,并在达到点B后,立即以同样的速度返回向点C运动;同时动点M从点B出发,沿折线B﹣A﹣C以1cm/s的速度向点C运动,当点N回到点C时,两个动点同时停止运动.⊙M是以M为圆心,1cm为半径的圆,设运动时间为t(s) (t>0)
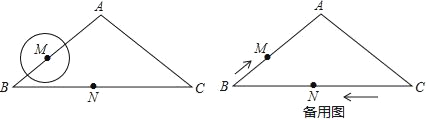
(1)tanB= ;
(2)当点M在线段AB上运动,且⊙M与BC相切时,求t的值;
(3)当t为何值时,⊙M与折线B﹣A﹣C的两个交点在等腰三角形ABC对称轴的同侧,且经过交点和点N的直线与⊙M相切?
-
科目: 来源: 题型:
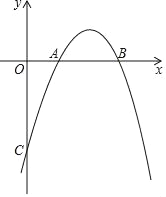
查看答案和解析>>【题目】己知,二次函数y=﹣x2+bx+c的图象与x轴的两个交点A,B的横坐标分别为1和2,与y轴的交点是C.
(1)求这个二次函数的表达式;
(2)若点D是y轴上的一点,是否存在D,使以B,C,D为顶点的三角形与△ABC相似?若存在,求点D的坐标,若不存在,请说明理由;
(3)过点C作CE∥x轴,与二次函数y=﹣x2+bx+c的图象相交于点E,点H是该二次函数图象上的动点,过点H作HF∥y轴,交线段BC于点F,试探究当点H运动到何处时,△CHF与△HFE的面积之和最大,求点H的坐标及最大面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在矩形 ABCD 中,动点 E 从点 A 出发,沿 AB→BC 方向运动,当点 E 到达点 C 时 停止运动.过点 E 作 FE⊥AE,交 CD 于 F 点,设点 E 运动路程为 x,FC=y,图②表示 y与 x 的函数关系的大致图像,则矩形 ABCD 的面积是( )

A.
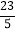 B. 5 C. 6 D.
B. 5 C. 6 D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】嘉兴某校组织了“垃圾分类”知识竞赛活动,获奖同学在竞赛中的成绩绘成如下图表,
根据图表提供的信息解答下列问题:
垃圾分类知识竞赛活动成绩统计表
分数段
频数
频数频率
80≤x<85
x
0.2
85≤x<90
80
y
90≤x<95
60
0.3
95≤x<100
20
0.1
(1)求本次获奖同学的人数;
(2)求表中x,y的数值:并补全频数分布直方图.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,边长为2的正方形纸片ABCD中,点M为边CD上一点(不与C,D重合),将△ADM沿AM折叠得到△AME,延长ME交边BC于点N,连结AN.
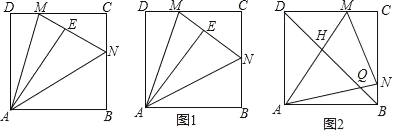
(1)猜想∠MAN的大小是否变化,并说明理由;
(2)如图1,当N点恰为BC中点时,求DM的长度;
(3)如图2,连结BD,分别交AN,AM于点Q,H.若BQ=
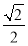 ,求线段QH的长度.
,求线段QH的长度. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图是一张平行四边形纸片ABCD,要求利用所学知识将它变成一个菱形,甲、乙两位同学的作法分别如下:
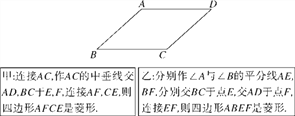
对于甲、乙两人的作法,可判断( )
A. 甲正确,乙错误 B. 甲错误,乙正确
C. 甲、乙均正确 D. 甲、乙均错误
相关试题

