【题目】画出函数y=2x+6的图象,利用图象:
(1)求方程2x+6=0的解;
(2)求不等式2x+6>0的解;
参考答案:
【答案】
(1)
解答: 依题意画出函数图象(如图)
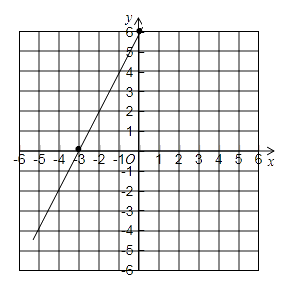
从图象可以看到,直线y=2x+6与x轴的交点坐标为(-3,0),
∴方程2x+6=0
解得:x=-3.
(2)
解答:如图当x>-3时,直线在x轴的上方,此时函数值大于0,
即:2x+6>0.
∴所求不等式的解为:x>-3
【解析】利用一次函数的关系式画出函数图象,根据函数图象与坐标轴的交点及函数图象的性质解答
【考点精析】掌握一次函数的图象和性质是解答本题的根本,需要知道一次函数是直线,图像经过仨象限;正比例函数更简单,经过原点一直线;两个系数k与b,作用之大莫小看,k是斜率定夹角,b与Y轴来相见,k为正来右上斜,x增减y增减;k为负来左下展,变化规律正相反;k的绝对值越大,线离横轴就越远.
-
科目: 来源: 题型:
查看答案和解析>>【题目】作出函数y=2x+6的图象并回答:
(1)x取何值时,y=0;
(2)x取何值时,y>0?
(3)x取何值时,y<0? -
科目: 来源: 题型:
查看答案和解析>>【题目】完成下面推理过程. 如图:在四边形ABCD中,∠A=106°﹣α,∠ABC=74°+α,BD⊥DC于点D,EF⊥DC于点F,求证:∠1=∠2
证明:∵∠A=106°﹣α,∠ABC=74°+α(已知)
∴∠A+∠ABC=180°
∴AD∥()
∴∠1=()
∵BD⊥DC,EF⊥DC(已知)
∴∠BDF=∠EFC=90°()
∴BD∥()
∴∠2=()
∴∠1=∠2()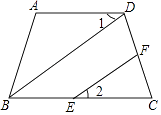
-
科目: 来源: 题型:
查看答案和解析>>【题目】商场进了一批商品,进价为每件800元,如果要保持销售利润不低于15%,则售价应不低于( ).
A. 900元 B. 920元 C. 960元 D. 980元
-
科目: 来源: 题型:
查看答案和解析>>【题目】有4根小棒,长度分别为2 cm,3 cm,4 cm,5 cm,任意取3根小棒首尾顺次相接搭三角形,可以搭出不同的三角形的个数为( )
A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠AGF=∠ABC,∠1+∠2=180°.

(1)试判断BF与DE的位置关系,并说明理由;
(2)若BF⊥AC,∠2=150°,求∠AFG的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】一元二次方程x2+x+1=0的根的情况是()
A.有两个不相等的实数根B.有两个相等的实数根
C.无实数根D.无法确定
相关试题

