【题目】如图,四边形ABCD和四边形ACED都是平行四边形,点R为DE的中点,BR分别交AC、CD于点P、Q.
(1)请写出图中各对相似三角形(相似比为1除外);
(2)求BP:PQ:QR.

参考答案:
【答案】(1)见解析;(2)3:1:2
【解析】试题分析:
(1)由平行四边形的性质结合相似三角形的判定定理可证得:①△BCP∽△BER;②△PCQ∽△RDQ;③△PCQ∽△PAB;④△PAB∽△RDQ;
(2)由(1)已知条件易证![]() ,结合R是DE的中点,易得
,结合R是DE的中点,易得![]() ,设BR=
,设BR= ![]() ,则BP=
,则BP= ![]() ,PQ=
,PQ= ![]() ,QR=
,QR= ![]() ,由此即可求得BP:PQ:QR的比值.
,由此即可求得BP:PQ:QR的比值.
试题解析:
(1)①∵四边形ACED是平行四边形,
∴∠BPC=∠BRE,∠BCP=∠E,
∴△BCP∽△BER;
②同理可得∠CDE=∠ACD,∠PQC=∠DQR,
∴△PCQ∽△RDQ;
③∵四边形ABCD是平行四边形,
∴∠BAP=∠PCQ,
∵∠APB=∠CPQ,
∴△PCQ∽△PAB;
④∵△PCQ∽△RDQ,△PCQ∽△PAB,
∴△PAB∽△RDQ.
综上所述,图中共有4对相似三角形,分别是:①△BCP∽△BER;②△PCQ∽△RDQ;③△PCQ∽△PAB;④△PAB∽△RDQ;
(2)∵四边形ABCD和四边形ACED都是平行四边形,
∴BC=AD=CE,
∵△BCP∽△BER,△PCQ∽△RDQ,
∴![]() ,
, ![]() ,
,
∵R是DE的中点,
∴RE=DR,
∴![]()
∴当设BR= ![]() 时,BP=
时,BP= ![]() ,PQ=
,PQ= ![]() ,QR=
,QR= ![]() ,
,
∴BP:PQ:QR= ![]() :
: ![]() :
: ![]() =3:1:2.
=3:1:2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在日常生活中如取款、上网等都需要密码,有一种用“因式分解法”产生的密码,方便记忆,原理是对于多项
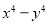 ,因式分解的结果是
,因式分解的结果是 ,若取
,若取 ,
,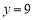 时,则各个因式的值是:
时,则各个因式的值是: ,
, ,
, ,于是就可以把“180162”作为一个六位数的密码,对于多项式
,于是就可以把“180162”作为一个六位数的密码,对于多项式 ,取
,取 ,
, 时,用上述方法产生的密码是________ (写出一个即可).
时,用上述方法产生的密码是________ (写出一个即可). -
科目: 来源: 题型:
查看答案和解析>>【题目】在大课间活动中,同学们积极参加体育锻炼,小龙在全校随机抽取一部分同学就“我最喜爱的体育项目”进行了一次抽样调查,下面是他通过收集的数据绘制的两幅不完整的统计图,请你根据图中提供的信息,解答以下问题:
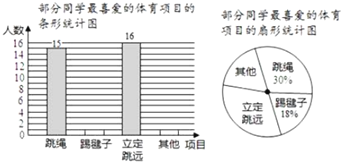
(1)小龙共抽取______名学生;
(2)补全条形统计图;
(3)在扇形统计图中,“其他”部分对应的圆心角的度数是_______;
(4)若全校共2100名学生,请你估算“立定跳远”部分的学生人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC中,BC边的长为x,BC边上的高为y,△ABC的面积为3.
(1)写出y关于x的函数关系式 ;x的取值范围是 .
(2)列表,得
x
…
1
2
3
4
…
y
…
…
在给出的坐标系中描点并连线;
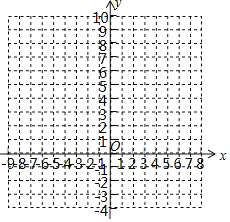
(3)如果A(x1,y1),B(x2,y2)是图象上的两个点,且x1>x2>0,试判断y1,y2的大小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数
 的图象经过点A(﹣3,6)、B(m,0)、C(3,0),并且m<3,D为抛物线的顶点.
的图象经过点A(﹣3,6)、B(m,0)、C(3,0),并且m<3,D为抛物线的顶点.(1)求b,c,m的值;
(2)设点P是线段OC上一点,点O是坐标原点,且满足∠PDC=∠BAC,求点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某文化中学教职工情况如下(单位:人):领导:9;教师:90;职员:15;工人:6.为了便于比较和统计,你能将该文化中学教职工的人数情况制成一幅扇形统计图吗?试试看.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,点A(﹣3,0),点B是x轴上异于点A一动点,设B(x,0),以AB为边在x轴的上方作正方形ABCD.

(1)如图(1),若点B(1,0),则点D的坐标为 ;
(2)若点E是AB的中点,∠DEF=90°,且EF交正方形外角的平分线BF于F.
①如图(2),当x>0时,求证:DE=EF;
②若点F的纵坐标为y,求y关于x的函数解析式.
相关试题

