【题目】在大课间活动中,同学们积极参加体育锻炼,小龙在全校随机抽取一部分同学就“我最喜爱的体育项目”进行了一次抽样调查,下面是他通过收集的数据绘制的两幅不完整的统计图,请你根据图中提供的信息,解答以下问题:
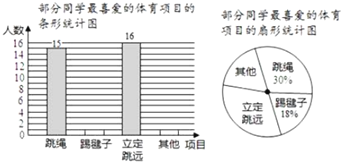
(1)小龙共抽取______名学生;
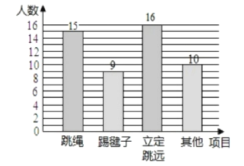
(2)补全条形统计图;
(3)在扇形统计图中,“其他”部分对应的圆心角的度数是_______;
(4)若全校共2100名学生,请你估算“立定跳远”部分的学生人数.
参考答案:
【答案】(1)50;(2)补图见解析;(3)72°;(4)672人.
【解析】
(1)画出统计图,根据跳绳的人数除以占的百分比即可得出抽取的学生总数;
(2)根据总学生数,求出踢毽子与其中的人数,补全条形统计图即可
(3)根据立定跳远占的百分比乘以360即可得到结果
(4)由其他占的百分比,乘以2100即可得到结果
(1)根据题意得:15÷30%=50(名)
则小明共抽取50名学生
(2)根据题意得:踢毽子人数为50×18%=9(名),其
他人数为50×(1-30%-18%-32%)=10名),
补全条形统计图,如图所示
(3)根据题意得:360°×20%=72°
则“其他"部分对应的圆心角的度数是72°;
(4)根据题意得'其他"部分的学生有
2100×32%=672(名)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某服装店购进一批甲、乙两种款型时尚T恤衫,甲种款型共用了7800元,乙种款型共用了6400元,甲种款型的件数是乙种款型件数的1.5倍,甲种款型每件的进价比乙种款型每件的进价少30元.
(1)甲、乙两种款型的T恤衫各购进多少件?
(2)商店进价提高60%标价销售,销售一段时间后,甲款型全部售完,乙款型剩余一半,商店决定对乙款型按标价的五折降价销售,很快全部售完,求售完 这批T恤衫商店共获利多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】大家见过形如x+y=z,这样的三元一次方程,并且知道x=3,y=4,z=7就是适合该方程的一个正整数解,法国数学家费尔马早在17世纪还研究过形如x2+y2=z2的方程.
(1)请写出方程x2+y2=z2的两组正整数解: .
(2)研究直角三角形和勾股数时,我国古代数学专著(九章算术)给出了如下数:a=
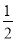 (m2﹣n2),b=mn,c=
(m2﹣n2),b=mn,c=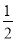 (m2+n2),(其中m>n,m,n是奇数),那么,以a,b,c为三边的三角形为直角三角形,请你加以验证.
(m2+n2),(其中m>n,m,n是奇数),那么,以a,b,c为三边的三角形为直角三角形,请你加以验证. -
科目: 来源: 题型:
查看答案和解析>>【题目】在日常生活中如取款、上网等都需要密码,有一种用“因式分解法”产生的密码,方便记忆,原理是对于多项
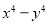 ,因式分解的结果是
,因式分解的结果是 ,若取
,若取 ,
,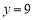 时,则各个因式的值是:
时,则各个因式的值是: ,
, ,
, ,于是就可以把“180162”作为一个六位数的密码,对于多项式
,于是就可以把“180162”作为一个六位数的密码,对于多项式 ,取
,取 ,
, 时,用上述方法产生的密码是________ (写出一个即可).
时,用上述方法产生的密码是________ (写出一个即可). -
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC中,BC边的长为x,BC边上的高为y,△ABC的面积为3.
(1)写出y关于x的函数关系式 ;x的取值范围是 .
(2)列表,得
x
…
1
2
3
4
…
y
…
…
在给出的坐标系中描点并连线;
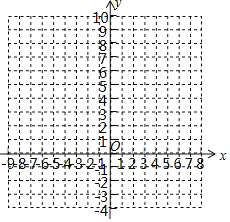
(3)如果A(x1,y1),B(x2,y2)是图象上的两个点,且x1>x2>0,试判断y1,y2的大小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD和四边形ACED都是平行四边形,点R为DE的中点,BR分别交AC、CD于点P、Q.
(1)请写出图中各对相似三角形(相似比为1除外);
(2)求BP:PQ:QR.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数
 的图象经过点A(﹣3,6)、B(m,0)、C(3,0),并且m<3,D为抛物线的顶点.
的图象经过点A(﹣3,6)、B(m,0)、C(3,0),并且m<3,D为抛物线的顶点.(1)求b,c,m的值;
(2)设点P是线段OC上一点,点O是坐标原点,且满足∠PDC=∠BAC,求点P的坐标.
相关试题

