【题目】已知,有理数![]() ,
,![]() ,
,![]() 在数轴上所对应的点分别是
在数轴上所对应的点分别是![]() ,
,![]() ,
,![]() 三点,且
三点,且![]() ,
,![]() ,
,![]() 满足;①
满足;①![]() ;②多项式
;②多项式![]() 是关于
是关于![]() 的二次三项式.
的二次三项式.
(1)![]() ,
,![]() ,
,![]() 的值分别是 (直接写出答案);
的值分别是 (直接写出答案);
(2)若数轴上点![]() ,
,![]() 之间有一动点
之间有一动点![]() ,且点
,且点![]() 对应的数为
对应的数为![]() ,化简
,化简![]() ;
;
(3)若点![]() 在数轴上以每秒1个单位的速度向左运动,同时点
在数轴上以每秒1个单位的速度向左运动,同时点![]() 和点
和点![]() 在数轴上分别以每秒
在数轴上分别以每秒![]() 个单位长度和4个单位长度的速度向右运动(其中
个单位长度和4个单位长度的速度向右运动(其中![]() ),若在整个运动过程中,点
),若在整个运动过程中,点![]() 到点
到点![]() 的距离与点
的距离与点![]() 到点
到点![]() 的距离差始终不变,求运动几秒后点
的距离差始终不变,求运动几秒后点![]() 与点
与点![]() 的距离为13个单位长度.
的距离为13个单位长度.
参考答案:
【答案】(1)-2,1,5;(2)4y-8;(3)t=4.
【解析】
(1)由非负性和二次三项式的定义可求a,b,c的值;
(2)由y的取值范围,化简可求解;
(3)先求出m的值,再由题意列出方程,求解即可.
(1)∵(b-1)2+|c-5|=0,
∴b=1,c=5,
∵多项式![]() x|a|+(a-2)x+7是关于x的二次三项式,
x|a|+(a-2)x+7是关于x的二次三项式,
∴a=-2,
故答案为:-2,1,5;
(2)∵数轴上点B、C之间有一动点P,
∴1<y<5;
∴|y|-2|y-5|+|y+2|=y-2(5-y)+y+2=4y-8;
(3)∵点B到点C的距离与点B到点A的距离差始终不变,
∴[(5+4t)-(1+mt)]-[(1+mt)-(-2-t)]=1+(3-2m)t是定值,
∴m=![]() ,
,
∵点B与点A的距离为13个单位长度.
∴(1+![]() t)-(-2-t)=13,
t)-(-2-t)=13,
∴t=4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,△ABC是等边三角形,AE=CD,BQ⊥AD于Q,BE交AD于点P.
(1)求证:△ABE≌△CAD;
(2)若PQ=2,BE=5,求PE的值.
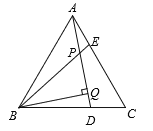
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,在△ABC中,∠ACB=90°,AC=BC,直线l过点C,点A,B在直线l同侧,BD⊥l,AE⊥l,垂足分别为D,E.求证:△AEC≌△CDB.
(2)如图2,AE⊥AB,且AE=AB,BC⊥CD,且BC=CD,利用(1)中的结论,请按照图中所标注的数据计算图中实线所围成的图形的面积S= .

-
科目: 来源: 题型:
查看答案和解析>>【题目】由于某地供水管爆裂.该地供水部门组织工人进行抢修.供水部门距离抢修工地15千米.抢修车装载着所需材料先从供水部门出发,15分钟后,工人乘吉普车从同一地点出发,结果他们同时到达抢修工地.已知吉普车速度是抢修车速度的1.5倍,求这两种车的速度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的盒子中放有四张卡片,每张卡片上写有一个实数,分别为2,
 ,
, ,1.(卡片除了实数不同外,其余均相同)
,1.(卡片除了实数不同外,其余均相同)(1)从盒子中随机抽取一张卡片,请直接写出卡片上的实数是有理数的概率;
(2)将卡片揺匀后先随机抽出一张,再从剩下的卡片中随机抽出一张,然后将抽取的两张卡片上的实数相乘,请你用列表法或树状图(树形图)法,求抽取的两张卡片上的实数之积为整数的概率。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AC的垂直平分线MN分别交AB,AC于D,E.若AE=5,△BCD的周长17,求△ABC的周长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,BC为弦,D为弧AC的中点,AC、BD相交于点E.AP交BD的延长线于点P.∠PAC=2∠CBD.
(1)求证:AP是⊙O的切线;
(2)若PD=3,AE=5,求△APE的面积.
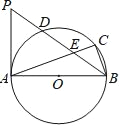
相关试题

