搜索
【题目】近一个月来我市遭受暴雨袭击，沱江水位上涨。小明以警戒水位为0点，用折线统计图表示某一天江水水位情况，请你结合折线统计图判断下列叙述不正确的是（ ）
A. 8时水位最高B. 8时到16时水位都在下降
C. 这一天水位均高于警戒水位D. P点表示12时水位高于警戒水位0.6米
参考答案：
【答案】B
【解析】
分析折线统计图表示每段时间中水位的高低，根据图形即可作出判断．
由折线统计图可知：8时水位为1.0米，是最高的；
从图中可以看出，在这一天中所有的水位都在0点以上，所以这一天水位均高于警戒水位；
8时到12时水位在下降，而12时到16时水位保持不变；
P点表示12时水位为0.6米，又知以警戒水位为0点，则P点表示12时水位高于警戒水位0.6米；
故选B．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在ABCD中，E、F分别是AB、CD的中点，AF与DE相交于点G，CE与BF相交于点H．
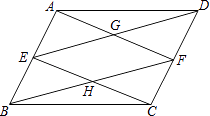
（1）求证：四边形EHFG是平行四边形；
（2）若四边形EHFG是矩形，则ABCD应满足什么条件？（不需要证明） -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，Rt△ABC的三个顶点分别是A（﹣3，2），B（0，4），C（0，2）．
（1）将△ABC以点C为旋转中心旋转180°，画出旋转后对应的△A1B1C1，平移△ABC，若点A的对应点A2的坐标为（0，﹣4），画出平移后对应的△A2B2C2；
（2）若将△A1B1C1绕某一点旋转可以得到△A2B2C2，请直接写出旋转中心的坐标．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图：在四边形ABCD中，AD∥BC，且BC=12cm，AD=18cm，P、Q分别从A、C同时出发，P以2cm/s的速度由A向D运动，Q以4cm/s的速度由C向B运动，问当多少秒时,直线QP将四边形ABCD截出一个平行四边形．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在直角坐标系中，直线y=x+m与y=
在第一象限交于点A，且与x轴交于点C，AB⊥x轴，垂足为B，且S△AOB=1．
（1）求m的值；
（2）求△ABC的面积． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，如果以正方形ABCD的对角线AC为边作第二个正方形ACEF，再以对角线AE为边作第三个正方形AEGH，如此下去，……，已知正方形ABCD的面积为S1为1，按上述方法所作的正方形的面积依次为S2，S3，……………，则Sn（n为正整数），那么第n个正方形的面积Sn等于（ ）
A.
B. 
C. 
D. 
-
科目： 来源： 题型：
查看答案和解析>>【题目】某地区为了进一步缓解交通拥堵问题，决定修建一条长为7千米的公路．如果平均每天的修建费y（万元）与修建天数x（天）在30≤x≤12 0之间时具有一次函数的关系，如下表所示．
x
50
60
90
120
y
40
38
32
26
（1）求y关于x的函数关系式；
（2）后来在修建的过程中计划发生改变，政府决定多修3千米，因此在没有增减建设力量的情况下，修完这条路比计划晚了15天，求原计划每天的修建费．
相关试题
