【题目】如图,在△ABC中,∠C=90°,点O在AC上,以OA为半径的⊙O交AB于点D,BD的垂直平分线交BC于点E,交BD于点F,连接DE.
(1)判断直线DE与⊙O的位置关系,并说明理由;
(2)若AC=6,BC=8,OA=2,求线段DE的长.

参考答案:
【答案】(1)直线DE与⊙O相切;(2)4.75.
【解析】试题分析:(1) 直线DE与⊙O相切,连接OD,根据等腰三角形的性质可得∠A=∠ODA,根据线段垂直平分线的性质及等腰三角形的性质易得∠B=∠EDB,易证ODA+∠EDB=![]() ,即可得∠ODE=
,即可得∠ODE=![]() -
-![]() =
=![]() ,所以直线DE与⊙O相切;(2)连接OE,设DE=x,则EB=ED=x,CE=8-x.因∠C=∠ODE =
,所以直线DE与⊙O相切;(2)连接OE,设DE=x,则EB=ED=x,CE=8-x.因∠C=∠ODE =![]() ,根据勾股定理可得
,根据勾股定理可得![]() ,即
,即![]() ,解得x的值即可得线段DE的长.
,解得x的值即可得线段DE的长.
试题解析: (1) 直线DE与⊙O相切.
理由如下:
连接OD,
∵OD=OA,
∴∠A=∠ODA.
∵EF是BD的垂直平分线,
∴EB="ED."
∴∠B=∠EDB.
∵∠C=![]() ,
,
∴∠A+∠B=![]() .
.
∴∠ODA+∠EDB=![]() .
.
∴∠ODE=![]() -
-![]() =
=![]() .
.
∴直线DE与⊙O相切.
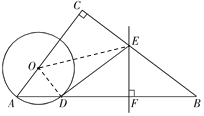
(2) 解法一:
连接OE,
设DE=x,则EB=ED=x,CE=8-x.
∵∠C=∠ODE =![]() ,
,
∴![]() .
.
∴![]() .
.
∴![]() .
.
即DE=![]() .
.
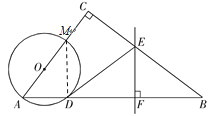
解法二:
连接DM,
∵AM是直径,
∴∠MDA=![]() ,AM=4.
,AM=4.
又∵∠C=![]() ,
,
∴![]() ,
,
![]() .
.
∴![]() , ∴AD=2.4.
, ∴AD=2.4.
∴BD=10-2.4=7.6.
∴BF=![]() .
.
∵EF⊥BD,∠C=![]() ,
,
∴![]() .
.
∴![]() , BE=
, BE=![]() .
.
∴DE=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】ABCD中,E是CD边上一点,
(1)将△ADE绕点A按顺时针方向旋转,使AD、AB重合,得到△ABF,如图1所示.观察可知:与DE相等的线段是 ,∠AFB=∠
(2)如图2,正方形ABCD中,P、Q分别是BC、CD边上的点,且∠PAQ=45°,试通过旋转的方式说明:DQ+BP=PQ;
(3)在(2)题中,连接BD分别交AP、AQ于M、N,你还能用旋转的思想说明BM2+DN2=MN2吗?

-
科目: 来源: 题型:
查看答案和解析>>【题目】2013贺州)地球距月球表面约为383900千米,那么这个距离用科学记数法应表示为千米.(结果保留三个有效数字)
-
科目: 来源: 题型:
查看答案和解析>>【题目】A,B,C三点高分别为-17.4米,-119米,-72.4米.
问:三点中最高点为哪一个?最低点为哪一个?最高点比最低点高多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的方程
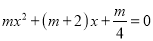 有两个不相等的实数根.
有两个不相等的实数根.(1)求m的取值范围;
(2)是否存在实数m,使方程的两个实数根的倒数和等于0?若存在,求出m的值;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简再求值:
(1)(4a2﹣3a)﹣(1﹣4a+4a2),其中a=﹣2
(2)﹣2(mn﹣3m2)﹣[m2﹣5(mn﹣m2)+2mn],其中m=1,n=﹣2. -
科目: 来源: 题型:
查看答案和解析>>【题目】在一次科技知识竞赛中,两组学生成绩统计如下表,通过计算可知两组的方差为
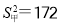 ,
,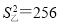 。下列说法:①两组的平均数相同;②甲组学生成绩比乙组学生成绩稳定;③甲组成绩的众数>乙组成绩的众数;④两组成绩的中位数均为80,但成绩≥80的人数甲组比乙组多,从中位数来看,甲组成绩总体比乙组好;⑤成绩高于或等于90分的人数乙组比甲组多,高分段乙组成绩比甲组好。其中正确的共有( ).
。下列说法:①两组的平均数相同;②甲组学生成绩比乙组学生成绩稳定;③甲组成绩的众数>乙组成绩的众数;④两组成绩的中位数均为80,但成绩≥80的人数甲组比乙组多,从中位数来看,甲组成绩总体比乙组好;⑤成绩高于或等于90分的人数乙组比甲组多,高分段乙组成绩比甲组好。其中正确的共有( ).分数
50
60
70
80
90
100
人
数
甲组
2
5
10
13
14
6
乙组
4
4
16
2
12
12
A.2种 B.3种 C.4种 D.5种
相关试题

