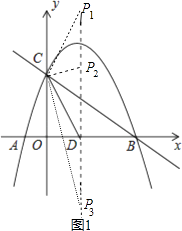
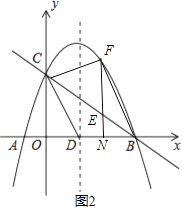
【题目】如图,抛物线y=﹣ ![]() x2+mx+n与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(﹣1,0),C(0,2).
x2+mx+n与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(﹣1,0),C(0,2).
(1)求抛物线的表达式;
(2)在抛物线的对称轴上是否存在点P,使△PCD是以CD为腰的等腰三角形?如果存在,直接写出P点的坐标;如果不存在,请说明理由;
(3)点E是线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时,四边形CDBF的面积最大?求出四边形CDBF的最大面积及此时E点的坐标.
参考答案:
【答案】
(1)
解:把A(﹣1,0),C(0,2)代入y=﹣ ![]() x2+mx+n得
x2+mx+n得 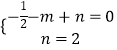 ,解得
,解得 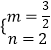 ,
,
∴抛物线解析式为y=﹣ ![]() x2+
x2+ ![]() x+2
x+2
(2)
解:存在.
抛物线的对称轴为直线x=﹣ 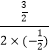 =
= ![]() ,
,
则D( ![]() ,0),
,0),
∴CD= ![]() =
= ![]() =
= ![]() ,
,
如图1,当CP=CD时,则P1( ![]() ,4);
,4);
当DP=DC时,则P2( ![]() ,
, ![]() ),P3(
),P3( ![]() ,﹣
,﹣ ![]() ),
),
综上所述,满足条件的P点坐标为( ![]() ,4)或(
,4)或( ![]() ,
, ![]() )或(
)或( ![]() ,﹣
,﹣ ![]() )
)
(3)
解:当y=0时,=﹣ ![]() x2+
x2+ ![]() x+2=0,解得x1=﹣1,x2=4,则B(4,0),
x+2=0,解得x1=﹣1,x2=4,则B(4,0),
设直线BC的解析式为y=kx+b,
把B(4,0),C(0,2)代入得 ![]() ,解得
,解得 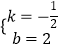 ,
,
∴直线BC的解析式为y=﹣ ![]() x+2,
x+2,
设E(x,﹣ ![]() x+2)(0≤x≤4),则F(x,﹣
x+2)(0≤x≤4),则F(x,﹣ ![]() x2+
x2+ ![]() x+2),
x+2),
∴FE=﹣ ![]() x2+
x2+ ![]() x+2﹣(﹣
x+2﹣(﹣ ![]() x+2)=﹣
x+2)=﹣ ![]() x2+2x,
x2+2x,
∵S△BCF=S△BEF+S△CEF= ![]() 4EF=2(﹣
4EF=2(﹣ ![]() x2+2x)=﹣x2+4x,
x2+2x)=﹣x2+4x,
而S△BCD= ![]() ×2×(4﹣
×2×(4﹣ ![]() )=
)= ![]() ,
,
∴S四边形CDBF=S△BCF+S△BCD
=﹣x2+4x+ ![]() (0≤x≤4),
(0≤x≤4),
=﹣(x﹣2)2+ ![]()
当x=2时,S四边形CDBF有最大值,最大值为 ![]() ,此时E点坐标为(2,1).
,此时E点坐标为(2,1).
【解析】(1)直接把A点和C点坐标代入y=﹣ ![]() x2+mx+n得m、n的方程组,然后解方程组求出m、n即可得到抛物线解析式;(2)先利用抛物线对称轴方程求出抛物线的对称轴为直线x=﹣
x2+mx+n得m、n的方程组,然后解方程组求出m、n即可得到抛物线解析式;(2)先利用抛物线对称轴方程求出抛物线的对称轴为直线x=﹣ ![]() ,则D(
,则D( ![]() ,0),则利用勾股定理计算出CD=
,0),则利用勾股定理计算出CD= ![]() ,然后分类讨论:如图1,当CP=CD时,利用等腰三角形的性质易得P1(
,然后分类讨论:如图1,当CP=CD时,利用等腰三角形的性质易得P1( ![]() ,4);当DP=DC时,易得P2(
,4);当DP=DC时,易得P2( ![]() ,
, ![]() ),P3(
),P3( ![]() ,﹣
,﹣ ![]() );(3)先根据抛物线与x轴的交点问题求出B(4,0),再利用待定系数法求出直线BC的解析式为y=﹣
);(3)先根据抛物线与x轴的交点问题求出B(4,0),再利用待定系数法求出直线BC的解析式为y=﹣ ![]() x+2,利用一次函数图象上点的坐标特征和二次函数图象上点的坐标特征,设E(x,﹣
x+2,利用一次函数图象上点的坐标特征和二次函数图象上点的坐标特征,设E(x,﹣ ![]() x+2)(0≤x≤4),则F(x,﹣
x+2)(0≤x≤4),则F(x,﹣ ![]() x2+
x2+ ![]() x+2),则FE=﹣
x+2),则FE=﹣ ![]() x2+2x,由于△BEF和△CEF共底边,高的和为4,则S△BCF=S△BEF+S△CEF=
x2+2x,由于△BEF和△CEF共底边,高的和为4,则S△BCF=S△BEF+S△CEF= ![]() 4EF=﹣x2+4x,加上S△BCD=
4EF=﹣x2+4x,加上S△BCD= ![]() ,所以S四边形CDBF=S△BCF+S△BCD=﹣x2+4x+
,所以S四边形CDBF=S△BCF+S△BCD=﹣x2+4x+ ![]() (0≤x≤4),然后根据二次函数的性质求四边形CDBF的面积最大,并得到此时E点坐标.
(0≤x≤4),然后根据二次函数的性质求四边形CDBF的面积最大,并得到此时E点坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小明想测山高和索道的长度.他在B处仰望山顶A,测得仰角∠B=31°,再往山的方向(水平方向)前进80m至索道口C处,沿索道方向仰望山顶,测得仰角∠ACE=39°.

(1)求这座山的高度(小明的身高忽略不计);
(2)求索道AC的长(结果精确到0.1m).
(参考数据:tan31°≈ ,sin31°≈
,sin31°≈  ,tan39°≈
,tan39°≈  ,sin39°≈
,sin39°≈  )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知反比例函数y=
 (k为常数,k≠1).
(k为常数,k≠1).
(Ⅰ)其图象与正比例函数y=x的图象的一个交点为P,若点P的纵坐标是2,求k的值;
(Ⅱ)若在其图象的每一支上,y随x的增大而减小,求k的取值范围;
(Ⅲ)若其图象的一支位于第二象限,在这一支上任取两点A(x1 , y1)、B(x2 , y2),当y1>y2时,试比较x1与x2的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知⊙O的直径为10,点A,点B,点C在⊙O上,∠CAB的平分线交⊙O于点D.

(Ⅰ)如图①,若BC为⊙O的直径,AB=6,求AC,BD,CD的长;
(Ⅱ)如图②,若∠CAB=60°,求BD的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,AB>AD,按以下步骤作图:以点A为圆心,小于AD的长为半径画弧,分别交AB、AD于点E、F;再分别以点E、F为圆心,大于
 EF的长为半径画弧,两弧交于点G;作射线AG交CD于点H,则下列结论中不能由条件推理得出的是( )
EF的长为半径画弧,两弧交于点G;作射线AG交CD于点H,则下列结论中不能由条件推理得出的是( ) 
A.AG平分∠DAB
B.AD=DH
C.DH=BC
D.CH=DH -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两名同学某学期的四次数学测试成绩(单位:分)如下表:
第一次
第二次
第三次
第四次
甲
87
95
85
93
乙
80
80
90
90
据上表计算,甲、乙两名同学四次数学测试成绩的方差分别为S甲2=17、S乙2=25,下列说法正确的是( )
A.甲同学四次数学测试成绩的平均数是89分
B.甲同学四次数学测试成绩的中位数是90分
C.乙同学四次数学测试成绩的众数是80分
D.乙同学四次数学测试成绩较稳定 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,按照三视图确定该几何体的侧面积是(图中尺寸单位:cm)( )

A.40πcm2
B.65πcm2
C.80πcm2
D.105πcm2
相关试题

