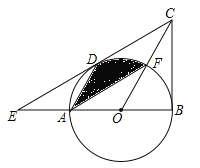
【题目】如图,在△BCE中,点A时边BE上一点,以AB为直径的⊙O与CE相切于点D,AD∥OC,点F为OC与⊙O的交点,连接AF.
(1)求证:CB是⊙O的切线;
(2)若∠ECB=60°,AB=6,求图中阴影部分的面积.
参考答案:
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题分析:(1)欲证明CB是⊙O的切线,只要证明BC⊥OB,可以证明△CDO≌△CBO解决问题.
(2)首先证明S阴=S扇形ODF,然后利用扇形面积公式计算即可.
试题解析:(1)证明:连接OD,与AF相交于点G,∵CE与⊙O相切于点D,∴OD⊥CE,∴∠CDO=90°,∵AD∥OC,∴∠ADO=∠1,∠DAO=∠2,∵OA=OD,∴∠ADO=∠DAO,∴∠1=∠2,在△CDO和△CBO中,∵CO=CO,∠1=∠2,OD=OC,∴△CDO≌△CBO,∴∠CBO=∠CDO=90°,∴CB是⊙O的切线.
(2)由(1)可知∠3=∠BCO,∠1=∠2,∵∠ECB=60°,∴∠3=![]() ∠ECB=30°,∴∠1=∠2=60°,∴∠4=60°,∵OA=OD,∴△OAD是等边三角形,∴AD=OD=OF,∵∠1=∠ADO,在△ADG和△FOG中,∵∠1=∠ADG,∠FGO=∠AGD,AD=OF,∴△ADG≌△FOG,∴S△ADG=S△FOG,∵AB=6,∴⊙O的半径r=3,∴S阴=S扇形ODF=
∠ECB=30°,∴∠1=∠2=60°,∴∠4=60°,∵OA=OD,∴△OAD是等边三角形,∴AD=OD=OF,∵∠1=∠ADO,在△ADG和△FOG中,∵∠1=∠ADG,∠FGO=∠AGD,AD=OF,∴△ADG≌△FOG,∴S△ADG=S△FOG,∵AB=6,∴⊙O的半径r=3,∴S阴=S扇形ODF=![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,对称轴为直线x=
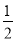 的抛物线经过B(2,0)、C(0,4)两点,抛物线与x轴的另一交点为A.
的抛物线经过B(2,0)、C(0,4)两点,抛物线与x轴的另一交点为A.(1)求抛物线的解析式;
(2)若点P为第一象限内抛物线上的一点,设四边形COBP的面积为S,求S的最大值;
(3)如图2,若M是线段BC上一动点,在x轴是否存在这样的点Q,使△MQC为等腰三角形且△MQB为直角三角形?若存在,求出点Q的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
 与x轴相交的于A,B两点(点A在点B的左侧),与y轴相交于点C,顶点为D.
与x轴相交的于A,B两点(点A在点B的左侧),与y轴相交于点C,顶点为D.(1)直接写出A,B,C三点的坐标和抛物线的对称轴;
(2)连接BC,与抛物线的对称轴交于点E,点P为线段BC上的一个动点(P不与C,B两点重合),过点P作PF∥DE交抛物线于点F,设点P的横坐标为m.
①用含m的代数式表示线段PF的长,并求出当m为何值时,四边形PEDF为平行四边形.
②设△BCF的面积为S,求S与m的函数关系式;当m为何值时,S有最大值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中,正确的是( )
A.三点确定一个圆
B.三角形有且只有一个外接圆
C.四边形都有一个外接圆
D.圆有且只有一个内接三角形 -
科目: 来源: 题型:
查看答案和解析>>【题目】己知x=1+3m,y=1-9m,用含x的式子表示y为:y= ______ .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c中,函数y与自变量x的部分对应值如表,则方程ax2+bx+c=0的一个解的范围是( )
x
6.17
6.18
6.19
6.20
y
﹣0.03
﹣0.01
0.02
0.04
A.﹣0.01<x<0.02
B.6.17<x<6.18
C.6.18<x<6.19
D.6.19<x<6.20 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程x2﹣2x+k=0的一个根是3,则另一个根是 .
相关试题

