【题目】已知,AB∥CD,点E为射线FG上一点. 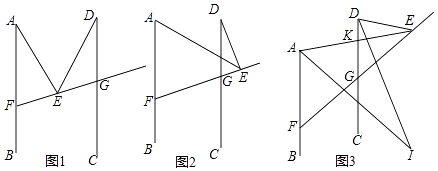
(1)如图1,直接写出∠EAF、∠AED、∠EDG之间的数量关系;
(2)如图2,当点E在FG延长线上时,求证:∠EAF=∠AED+∠EDG;
(3)如图3,AI平分∠BAE,DI交AI于点I,交AE于点K,且∠EDI:∠CDI=2:1,∠AED=20°,∠I=30°,求∠EKD的度数.
参考答案:
【答案】
(1)解:∠AED=∠EAF+∠EDG.
理由:如图1,过E作EH∥AB,
∵AB∥CD,
∴AB∥CD∥EH,
∴∠EAF=∠AEH,∠EDG=∠DEH,
∴∠AED=∠AEH+∠DEH=∠EAF+∠EDG;
(2)解:证明:如图2,设CD与AE交于点H,
∵AB∥CD,
∴∠EAF=∠EHG,
∵∠EHG是△DEH的外角,
∴∠EHG=∠AED+∠EDG,
∴∠EAF=∠AED+∠EDG;
(3)解:)∵AI平分∠BAE,
∴可设∠EAI=∠BAI=α,则∠BAE=2α,
∵AB∥CD,
∴∠CHE=∠BAE=2α,
∵∠AED=20°,∠I=30°,∠DKE=∠AKI,
∴∠EDI=α+30°﹣20°=α+10°,
又∵∠EDI:∠CDI=2:1,
∴∠CDI= ![]() ∠EDK=
∠EDK= ![]() α+5°,
α+5°,
∵∠CHE是△DEH的外角,
∴∠CHE=∠EDH+∠DEK,
即2α= ![]() α+5°+α+10°+20°,
α+5°+α+10°+20°,
解得α=70°,
∴∠EDK=70°+10°=80°,
∴△DEK中,∠EKD=180°﹣80°﹣20°=80°.
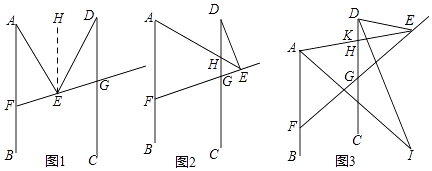
【解析】(1)过E作EH∥AB,根据两直线平行,内错角相等,即可得出∠AED=∠AEH+∠DEH=∠EAF+∠EDG;(2)设CD与AE交于点H,根据∠EHG是△DEH的外角,即可得出∠EHG=∠AED+∠EDG,进而得到∠EAF=∠AED+∠EDG;(3)设∠EAI=∠BAI=α,则∠CHE=∠BAE=2α,进而得出∠EDI=α+10°,∠CDI= ![]() α+5°,再根据∠CHE是△DEH的外角,可得∠CHE=∠EDH+∠DEK,即2α=
α+5°,再根据∠CHE是△DEH的外角,可得∠CHE=∠EDH+∠DEK,即2α= ![]() α+5°+α+10°+20°,求得α=70°,即可根据三角形内角和定理,得到∠EKD的度数.
α+5°+α+10°+20°,求得α=70°,即可根据三角形内角和定理,得到∠EKD的度数.
【考点精析】关于本题考查的平行线的性质和三角形的内角和外角,需要了解两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补;三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一元二次方程2x2﹣7x﹣1=0的根的情况是( )
A.有两个不相等的实数根B.有两个相等的实数根
C.没有实数根D.不能确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】在下列事件中,是必然事件的是
A. 买一张电影票,座位号一定是偶数
B. 随时打开电视机,正在播新闻
C. 将△ACB绕点C旋转50°得到△A′C′B′,这两个三角形全等
D. 阴天就一定会下雨
-
科目: 来源: 题型:
查看答案和解析>>【题目】某景点的门票价格如表:
购票人数/人
1~50
51~100
100以上
每人门票价/元
12
10
8
某校七年级(1)、(2)两班计划去游览该景点,其中(1)班人数少于50人,(2)班人数多于50人且少于100人,如果两班都以班为单位单独购票,则一共支付1118元;如果两班联合起来作为一个团体购票,则只需花费816元.
(1)两个班各有多少名学生?
(2)团体购票与单独购票相比较,两个班各节约了多少钱? -
科目: 来源: 题型:
查看答案和解析>>【题目】若△ABC与△DEF的相似比是3:2,△DEF的最长边是6cm,那么△ABC的最长边是( )
A.4cm
B.9cm
C.4cm或9cm
D.以上答案都不对 -
科目: 来源: 题型:
查看答案和解析>>【题目】钓鱼岛是我国固有领土,位于我国东海,总面积约6340000平方米,数据6340000用科学记数法表示为( )
A.634×104
B.6.34×106
C.63.4×105
D.6.34×107 -
科目: 来源: 题型:
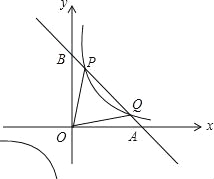
查看答案和解析>>【题目】已知直线y=kx+b与x轴、y轴分别交于A、B两点,与反比例函数交于一象限内的P(
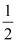 ,n),Q(4,m)两点,且tan∠BOP=
,n),Q(4,m)两点,且tan∠BOP=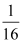 :
:(1)求反比例函数和直线的函数表达式;
(2)求△OPQ的面积.
相关试题

