【题目】在![]() 中,
中,![]() ,在
,在![]() 的外部作等边三角形
的外部作等边三角形![]() ,
,![]() 为
为![]() 的中点,连接
的中点,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,连接
,连接![]() .
.
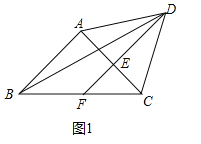
(1)如图1,若![]() ,求
,求![]() 的度数;
的度数;
(2)如图2,![]() 的平分线交
的平分线交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() .
.
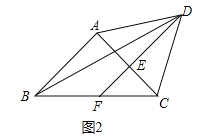
①补全图2;
②若![]() ,求证:
,求证:![]() .
.
参考答案:
【答案】(1)![]() ;(2)①补全图形,如图所示.见解析;②见解析.
;(2)①补全图形,如图所示.见解析;②见解析.
【解析】
(1)分别求出∠ADF,∠ADB,根据∠BDF=∠ADF-∠ADB计算即可;
(2)①根据要求画出图形即可;
②设∠ACM=∠BCM=α,由AB=AC,推出∠ABC=∠ACB=2α,可得∠NAC=∠NCA=α,∠DAN=60°+α,由△ABN≌△ADN(SSS),推出∠ABN=∠ADN=30°,∠BAN=∠DAN=60°+α,∠BAC=60°+2α,在△ABC中,根据∠BAC+∠ACB+∠ABC=180°,构建方程求出α,再证明∠MNB=∠MBN即可解决问题;
(1)解:如图1中,
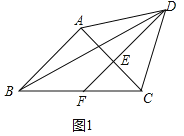
在等边三角形![]() 中,
中,
![]() ,
,![]() .
.
∵![]() 为
为![]() 的中点,
的中点,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
(2)①补全图形,如图所示.
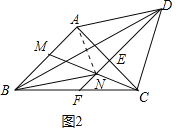
②证明:连接![]() .
.
∵![]() 平分
平分![]() ,
,
∴设![]() ,
,
∵![]() ,
,
∴![]() .
.
在等边三角形![]() 中,
中,
∵![]() 为
为![]() 的中点,
的中点,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中,
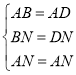
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]()
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
-
科目: 来源: 题型:
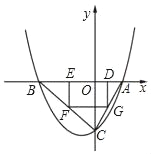
查看答案和解析>>【题目】如图,抛物线y=ax2+bx﹣4(a≠0)与x轴交于A(2,0)、B(﹣4,0)两点,与y轴交于点C,矩形DEFG的一条边DE在线段AB上,顶点F,G分别在线段BC、AC上.
(I)求抛物线的解析式;
(II)若点D的坐标为(m,0),矩形DEFG的面积为S,求S与m的函数关系式,并指出m的取值范围;
(III)当矩形DEFG的面积S取最大值时,连接DF并延长至点M,使FM=kDF.若点M在抛物线上,求k的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】从边长为
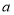 的正方形中剪掉一个边长为
的正方形中剪掉一个边长为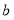 的正方形(如图1),然后将剩余部分拼成一个长方形(如图2).
的正方形(如图1),然后将剩余部分拼成一个长方形(如图2).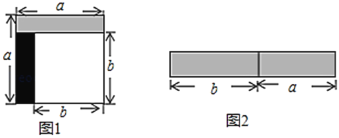
(1)探究:上述操作能验证的等式是:(请选择正确的一个)
A.
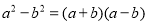 B.
B. C.
C.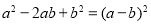
(2)应用:利用你从(1)选出的等式,完成下列各题:
①已知
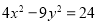 ,
,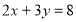 ,求
,求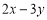 的值;
的值;②计算:
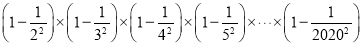 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】某市对城区部分路段的人行道地砖、绿化带、排水管等公用设施进行全面更新改造,根据市政建设的需要,需在35天内完成工程.现有甲、乙两个工程队有意承包这项工程,经调查知道,乙工程队单独完成此项工程的时间是甲工程队单独完成此项工程时间的2倍,若甲、乙两工程队合作,只需10天完成.
(1)甲、乙两个工程队单独完成此项工程各需多少天?
(2)若甲工程队每天的工程费用是4万元,乙工程队每天的工程费用是2.5万元,请你设计一种方案,既能按时完工,又能使工程费用最少.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点D在△ABC边延长线上,点O是边AC上一个动点,过O作直线EF∥BC,交∠BCA的平分线于点F,交∠BCA的外角平分线于E.当点O在线段AC上移动(不与点A,C重合)时,下列结论不一定成立的是( )
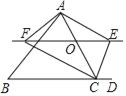
A. 2∠ACE=∠BAC+∠B B. EF=2OC C. ∠FCE=90° D. 四边形AFCE是矩形
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等腰三角形一腰上的中线将这个等腰三角形的周长分为9
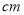 和15
和15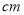 两部分,则这个等腰三角形的腰长为__________
两部分,则这个等腰三角形的腰长为__________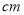 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,
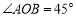 ,点
,点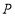 为
为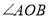 内部一点,点
内部一点,点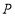 关于
关于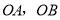 的对称点
的对称点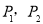 的连线交
的连线交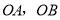 于
于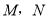 两点,连接
两点,连接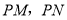 ,若
,若 ,则
,则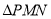 的周长=__________.
的周长=__________.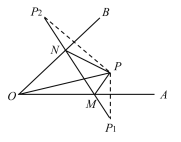
相关试题

