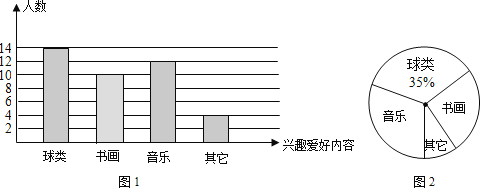
【题目】小李对初三(1)班全体同学的业余兴趣爱好(第一爱好)进行了一次调查,她根据采集到的数据,绘制了下面的图1和图2.

请你根据图中提供的信息,解答下列问题:
(1)初三(1)班共有学生________人;
(2)在图1中,将“书画”部分的图形补充完整;
(3)在图2中,“球类”部分所对应的圆心角的度数________度;爱好“音乐”的人数占本班学生数的百分数是________;爱好“书画”的人数占本班学生数的百分数是________;“其它”的人数占本班学生数的百分数是________.
参考答案:
【答案】(1)40;(2)详见解析;(3)126;30%;25%;10%
【解析】
(1)总人数=球类人数÷球类百分比;
(2)用总人数减去其他各项人数可得书画的人数,补全图形;
(3)将“球类”部分所对应的百分比乘以360度可得圆心角度数,分别将各类人数除以总人数可得百分比.
(1)初三(1)班共有学生14÷35%=40(人);
(2)选择书画的人数为:40-(14+12+4)=10(人),
补全图象如下:
(3)“球类”部分所对应的圆心角的度数为360°×35%=126°,
爱好“音乐”的人数占本班学生数的百分数是:![]() ×100%=30%,
×100%=30%,
爱好“书画”的人数占本班学生数的百分数是:![]() ×100%=25%,
×100%=25%,
“其它”的人数占本班学生数的百分数是:![]() ×100%=10%.
×100%=10%.
-
科目: 来源: 题型:
查看答案和解析>>【题目】课题小组从某市20000名九年级男生中,随机抽取了1000名进行50米跑测试,并根据测试结果绘制了如下尚不完整的统计图表.
等级
人数/名
优秀
a
良好
b
及格
150
不及格
50
解答下列问题:
(1)a等于多少?,b等于多少?
(2)补全条形统计图;
(3)试估计这20000名九年级男生中50米跑达到良好和优秀等级的总人数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,点E,F分别在边AB,BC上,且AE=
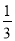 AB,将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,连接BP交EF于点Q,对于下列结论:①EF=2BE;②PF=2PE;③FQ=4EQ;④△PBF是等边三角形.其中正确的是 。
AB,将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,连接BP交EF于点Q,对于下列结论:①EF=2BE;②PF=2PE;③FQ=4EQ;④△PBF是等边三角形.其中正确的是 。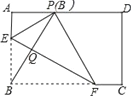
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠B=90°,直线EF分别交两直角边AB、BC与E、F两点,且EF∥AC,P是斜边AC的中点,连接PE,PF,且AB=
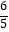 ,BC=
,BC= 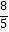 .
.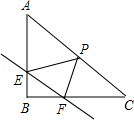
(1)当E、F均为两直角边的中点时,求证:四边形EPFB是矩形,并求出此时EF的长;
(2)设EF的长度为x(x>0),当∠EPF=∠A时,用含x的代数式表示EP的长;
(3)设△PEF的面积为S,则当EF为多少时,S有最大值,并求出该最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC内接于⊙O,∠A的度数为60°,∠ABC、∠ACB的角平分线分别交于AC、AB于点D、E,CE、BD相交于点F.以下四个结论:①cos∠BFE=
 ;②BC=BD;③EF=FD;④BF=2DF.其中结论一定正确的序号数是( )
;②BC=BD;③EF=FD;④BF=2DF.其中结论一定正确的序号数是( ) 
A.①②
B.①③
C.③④
D.②④ -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把一张矩形的纸ABCD沿对角线BD折叠,使点C落在点E处,BE与AD交于点F.
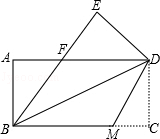
(1)求证:△ABF≌△EDF;
(2)若将折叠的图形恢复原状,点F与BC边上的点M正好重合,连接DM,试判断四边形BMDF的形状,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】小明在学习了数据的收集、整理与描述后,为妈妈整理记录了10月份的家庭支出情况,并绘制成如下尚不完整的统计图表,请你根据图表信息完成下列各题:
项目
物业费
伙食费
服装费
其他费
金额/元
800
400
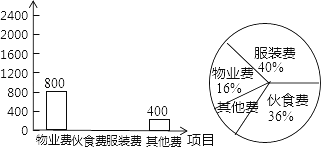
(1)10月份小明家共支出多少元?
(2)在扇形统计图中,表示“其他费”的扇形圆心角为多少度?
(3)请将表格补充完整;
项目
物业费
伙食费
服装费
其他费
金额/元
800
________
________
400
(4)请将条形统计图补充完整.
相关试题

