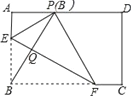
【题目】如图,在矩形ABCD中,点E,F分别在边AB,BC上,且AE=![]() AB,将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,连接BP交EF于点Q,对于下列结论:①EF=2BE;②PF=2PE;③FQ=4EQ;④△PBF是等边三角形.其中正确的是 。
AB,将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,连接BP交EF于点Q,对于下列结论:①EF=2BE;②PF=2PE;③FQ=4EQ;④△PBF是等边三角形.其中正确的是 。
参考答案:
【答案】① ④
【解析】试题解析:由折叠可得PE=BE,PF=BF,∠PEF=∠BEF,∠EFB=∠EFP,
∵AE=![]() AB,
AB,
∴BE=PE=2AE,
∴∠APE=30°,
∴∠PEF=∠BEF=60°,
∴∠EFB=∠EFP=30°,
∴EF=2BE,PF=![]() PE,
PE,
∴①正确,②不正确;
又∵EF⊥BP,
∴EF=2BE=4EQ,
∴③不正确;
又∵PF=BF,∠BFP=2∠EFP=60°,
∴△PBF为等边三角形,
∴④正确;
所以正确的为①④,
故答案为:①④.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,ABCD是正方形,G是BC上(除端点外)的任意一点,DE⊥AG于点E,BF∥DE,交AG于点F.下列结论不一定成立的是【 】
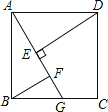
A.△AED≌△BFA B.DE﹣BF=EF C.△BGF∽△DAE D.DE﹣BG=FG
-
科目: 来源: 题型:
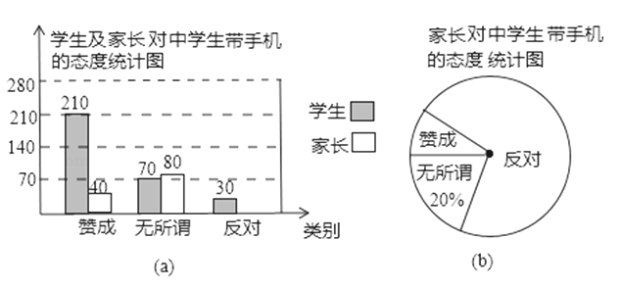
查看答案和解析>>【题目】“校园手机”现象越来越受到社会的关注,记者张丽利用周末时间随机调查了某校若干名家长对中学生带手机现象的看法,统计整理并制作了如下的统计图,根据统计图信息完成下列问题:
(1)这次一共随机抽查了多少个学生家长进行调查;
(2)请将条形图补充完整;在扇形统计图中表示“赞成”的圆心角等于多少度;
(3)如果某校有3000名中学生家长,持“反对”态度的学生家长大约有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】课题小组从某市20000名九年级男生中,随机抽取了1000名进行50米跑测试,并根据测试结果绘制了如下尚不完整的统计图表.
等级
人数/名
优秀
a
良好
b
及格
150
不及格
50
解答下列问题:
(1)a等于多少?,b等于多少?
(2)补全条形统计图;
(3)试估计这20000名九年级男生中50米跑达到良好和优秀等级的总人数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠B=90°,直线EF分别交两直角边AB、BC与E、F两点,且EF∥AC,P是斜边AC的中点,连接PE,PF,且AB=
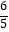 ,BC=
,BC= 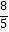 .
.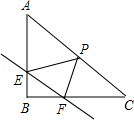
(1)当E、F均为两直角边的中点时,求证:四边形EPFB是矩形,并求出此时EF的长;
(2)设EF的长度为x(x>0),当∠EPF=∠A时,用含x的代数式表示EP的长;
(3)设△PEF的面积为S,则当EF为多少时,S有最大值,并求出该最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】小李对初三(1)班全体同学的业余兴趣爱好(第一爱好)进行了一次调查,她根据采集到的数据,绘制了下面的图1和图2.

请你根据图中提供的信息,解答下列问题:
(1)初三(1)班共有学生________人;
(2)在图1中,将“书画”部分的图形补充完整;
(3)在图2中,“球类”部分所对应的圆心角的度数________度;爱好“音乐”的人数占本班学生数的百分数是________;爱好“书画”的人数占本班学生数的百分数是________;“其它”的人数占本班学生数的百分数是________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC内接于⊙O,∠A的度数为60°,∠ABC、∠ACB的角平分线分别交于AC、AB于点D、E,CE、BD相交于点F.以下四个结论:①cos∠BFE=
 ;②BC=BD;③EF=FD;④BF=2DF.其中结论一定正确的序号数是( )
;②BC=BD;③EF=FD;④BF=2DF.其中结论一定正确的序号数是( ) 
A.①②
B.①③
C.③④
D.②④
相关试题

