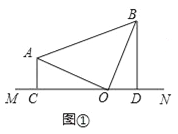
【题目】在△ABC中,∠AOB=90°,AO=BO,直线MN经过点O,且AC⊥MN于C,BD⊥MN于D
(1)当直线MN绕点O旋转到图①的位置时,求证:CD=AC+BD;
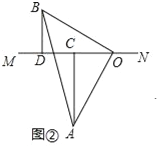
(2)当直线MN绕点O旋转到图②的位置时,求证:CD=AC﹣BD;
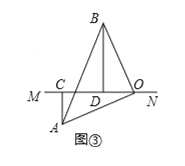
(3)当直线MN绕点O旋转到图③的位置时,试问:CD、AC、BD有怎样的等量关系?请写出这个等量关系,并加以证明.
参考答案:
【答案】(1)证明见解析;(2)证明见解析;(3)CD=BD﹣AC,证明见解析.
【解析】试题分析:(1)通过证明△ACO≌△ODB得到OC=BD,AC=OD,则CD=AC+BD;
(2)通过证明△ACO≌△ODB得到OC=BD,AC=OD,则CD=AC-BD;
(3)通过证明△ACO≌△ODB得到OC=BD,AC=OD,则CD=BD-AC.
试题解析:(1)如图1,
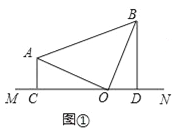
∵△AOB中,∠AOB=90°,
∴∠AOC+∠BOD=90°,
直线MN经过点O,且AC⊥MN于C,BD⊥MN于D,
∴∠ACO=∠BDO=90°
∴∠AOC+∠OAC=90°,
∴∠OAC=∠BOD,
在△ACO和△ODB中,
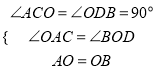
∴△ACO≌△ODB(AAS),
∴OC=BD,AC=OD,
∴CD=AC+BD;
(2)如图2,
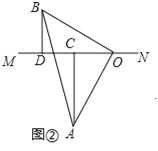
∵△AOB中,∠AOB=90°,
∴∠AOC+∠BOD=90°,
直线MN经过点O,且AC⊥MN于C,BD⊥MN于D,
∴∠ACO=∠BDO=90°
∴∠AOC+∠OAC=90°,
∴∠OAC=∠BOD,
在△ACO和△ODB中,
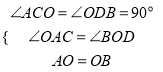 ,
,
∴△ACO≌△ODB(AAS),
∴OC=BD,AC=OD,
∴CD=OD﹣OC=AC﹣BD,即CD=AC﹣BD.
(3)如图3,
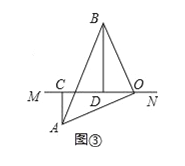
∵△AOB中,∠AOB=90°,
∴∠AOC+∠BOD=90°,
直线MN经过点O,且AC⊥MN于C,BD⊥MN于D,
∴∠ACO=∠BDO=90°
∴∠AOC+∠OAC=90°,
∴∠OAC=∠BOD,
在△ACO和△ODB中,
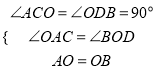 ,
,
∴△ACO≌△ODB(AAS),
∴OC=BD,AC=OD,
∴CD=OC﹣OD=BD﹣AC,
即CD=BD﹣AC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】地球的表面积约为51000000km,将51009000用科学记数法表示为( )
A. 0.51x109 B. 5.1×109 C. 5.1×108 D. 0.51×107
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一次函数y=(2﹣m)x﹣2的函数值y随x的增大而减小,则m的取值范围是( )
A.m<0
B.m>0
C.m<2
D.m>2 -
科目: 来源: 题型:
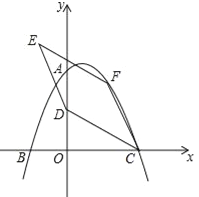
查看答案和解析>>【题目】如图,在平面直角坐标系中,二次函数
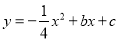 的图象与坐标轴交于A、B、C三点,其中点A的坐标为(0,8),点B的坐标为(﹣4,0).
的图象与坐标轴交于A、B、C三点,其中点A的坐标为(0,8),点B的坐标为(﹣4,0).(1)求该二次函数的表达式及点C的坐标;
(2)点D的坐标为(0,4),点F为该二次函数在第一象限内图象上的动点,连接CD、CF,以CD、CF为邻边作平行四边形CDEF,设平行四边形CDEF的面积为S.
①求S的最大值;
②在点F的运动过程中,当点E落在该二次函数图象上时,请直接写出此时S的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】第一宇宙速度约为7919.5959493米/秒,将它保留两个有效数字后的近似数是______________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】住建部发布数据显示,全国城市年度节约用水量约为65亿立方米,数据“65亿”用科学记数法表示为( )
A.0.65×102B.65×108C.6.5×109D.0.65×1010
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A. 任何一个有理数的绝对值都是正数
B. 有理数可以分为正有理数和负有理数
C. 多顶式3πa3+4a2-8的次数是4
D. x的系数和次数都是1
相关试题

