【题目】如图,四边形ABCD内接于以BC为直径的圆O,且AB=AD,延长CB、DA交于P,当PB=BO,CD=18时,求:
(1)⊙O的半径长;
(2)PA的长。
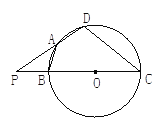
参考答案:
【答案】(1)12 (2)![]()
【解析】试题分析:(1)连接OA、BD交于F,由BC是 O的直径可以知道∠BDC=90°,而OA是半径,AB=AD根据垂径定理可以知道OA⊥BD,所以OA∥CD;接着可以得到![]() ;而PB=BO=OC,CD=18;现在可以求出OA了,也就求出了圆的半径.(2)由OF∥CD,OB=OC根据中位线定理可以求出OF,AF;在根据勾股定理在Rt△DBC中可以求出BD,DF;接着在Rt△ADF中求出AD;然后利用平行线的性质得∠FAD=∠CDE证明△AFD∽△DEC,利用相似三角形的对应边成比例可以求出DE了.
;而PB=BO=OC,CD=18;现在可以求出OA了,也就求出了圆的半径.(2)由OF∥CD,OB=OC根据中位线定理可以求出OF,AF;在根据勾股定理在Rt△DBC中可以求出BD,DF;接着在Rt△ADF中求出AD;然后利用平行线的性质得∠FAD=∠CDE证明△AFD∽△DEC,利用相似三角形的对应边成比例可以求出DE了.
试题解析: (1)连接OA,BD交于F,
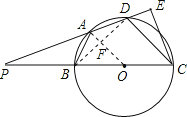
∵BC是O的直径,
∴∠BDC=90;
又∵OA是半径,AB=AD;
∴OA⊥BD,OA∥CD;
∵![]() ;
;
∴OA=12;
∴O的半径为12.
(2)∵OF∥CD, ![]() ;
;
∴OF=9,AF=3;
∵BD=![]() ;
;
∴DF= ![]() BD=
BD= ![]() ;
;
∴AD=![]()
∵OA∥CD;
∴![]() ,
,
∴AP=2AD=![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】点A(﹣3,2)关于x轴的对称点A′的坐标为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,E为BC边的中点,CD⊥AB,AB=2,AC=1,DE=
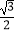 ,则∠CDE+∠ACD=( )
,则∠CDE+∠ACD=( ) 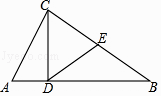
A.60°
B.75°
C.90°
D.105° -
科目: 来源: 题型:
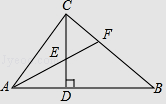
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,AF平分∠CAB,交CD于点E,交CB于点F.若AC=3,AB=5,则CE的长为( )
A.
B.
C.
D.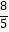
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a2+a﹣3=0,那么a2(a+4)的值是( )
A.﹣18
B.﹣15
C.﹣12
D.9 -
科目: 来源: 题型:
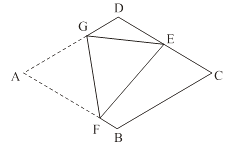
查看答案和解析>>【题目】如图,在菱形纸片ABCD中,AB=2,∠A=60°,将菱形纸片翻折,使点A落在CD的中点E处,折痕为FG,点F、G分别在边AB、AD上.则cos∠EFG的值为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠A=70°,下列角中是∠A的补角的是( )
A. 70°B. 110°C. 20°D. 180°
相关试题

