【题目】如图,在菱形纸片ABCD中,AB=2,∠A=60°,将菱形纸片翻折,使点A落在CD的中点E处,折痕为FG,点F、G分别在边AB、AD上.则cos∠EFG的值为 . 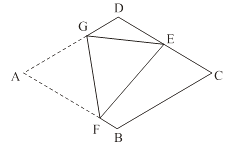
参考答案:
【答案】![]()
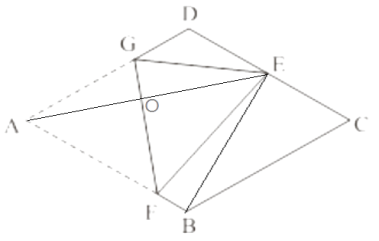
【解析】解:连接BE、AE交FG于点O,
∵菱形ABCD中,AB=2,∠A=60°,E为CD中点,
∴BE⊥CD,CE=1,BC=2,∠C=60°,∠ABC=120°,
∴BE=![]() ,∠CBE=30°,
,∠CBE=30°,
∴∠FBE=90°,
∴AE=![]() =
=![]() =
=![]() .
.
∵△AGF翻折至△EGF,
∴△AGF≌△EGF,
∴AF=EF,∠AFG=∠EFG,
在Rt△EBF中,设BF=x,则AF=EF=2-x,
∴(2-x)2=x2+(![]() )2
)2
∴x=![]() ,EF=
,EF=![]() ,
,
又∵AG=EG,AF=EF,
∴GF垂直平分AE,
∴EO=![]() .
.
∴FO=![]() =
=![]() =
=![]()
在Rt△EOF中.
∴cos∠EFG=![]() =
=![]() .
.
所以答案是:![]() .
.
【考点精析】掌握等腰三角形的性质和勾股定理的概念是解答本题的根本,需要知道等腰三角形的两个底角相等(简称:等边对等角);直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.
-
科目: 来源: 题型:
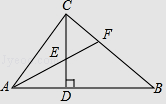
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,AF平分∠CAB,交CD于点E,交CB于点F.若AC=3,AB=5,则CE的长为( )
A.
B.
C.
D.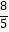
-
科目: 来源: 题型:
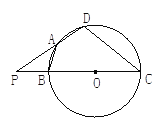
查看答案和解析>>【题目】如图,四边形ABCD内接于以BC为直径的圆O,且AB=AD,延长CB、DA交于P,当PB=BO,CD=18时,求:
(1)⊙O的半径长;
(2)PA的长。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a2+a﹣3=0,那么a2(a+4)的值是( )
A.﹣18
B.﹣15
C.﹣12
D.9 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠A=70°,下列角中是∠A的补角的是( )
A. 70°B. 110°C. 20°D. 180°
-
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x的一元二次方程ax2+2x﹣1=0无解,则a的取值范围是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,a,b,c分别是ΔABC中∠A,∠B,∠C的对边,P为BC上一点,以AP为直径的圆O交AB于D,PE∥AB交AC于E,b,c是方程x2+kx+9=0的两根,且(b2+c2)(b2+c2-14)-72=0,锐角B的正弦值等于
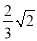 。
。(1)求K的值;
(2)设BD=x,求四边形ADPE的面积为S关于x的函数关系式;
(3)问圆O是否能与BC相切?若能请求出x的值;若不能,请说明理由。

相关试题

